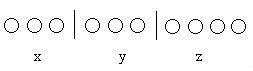定義
隔板法就是在n個元素間插入(b-1)個板,即把n個元素分成b組的方法。
問題解析
例1將20個大小形狀完全相同的小球放入3個不同的盒子,允許有盒子為空,但球必須放完,有多少種不同的方法?
分析:本題中的小球大小形狀完全相同,故這些小球沒有區別,問題等價於將小球分成三組,允許有若干組無元素,用隔板法.
解析:將20個小球分成三組需要兩塊隔板,因為允許有盒子為空,不符合隔板法的原理,那就人為的再加上3個小球,保證每個盒子都至少分到一個小球,那就符合隔板法的要求了(分完後,再在每組中各去掉一個小球,即滿足了題設的要求)。然後就變成待分小球總數為23個,球中間有22個空檔,需要在這22個空檔里加入2個隔板來分隔為3份,共有C(22,2)=231種不同的方法.
點評:對n件相同物品(或名額)分給m個人(或位置),允許若干個人(或位置)為空的問題,可以看成將這n件物品分成m組,允許若干組為空的問題.將n件物品分成m組,需要m-1塊隔板,將這n件物品和m-1塊隔板排成一排,占n+m-1位置,從這n+m-1個位置中選m-1個位置放隔板,因隔板無差別,故隔板之間無序,是組合問題,故隔板有Cn+m-1 m-1種不同的方法,再將物品放入其餘位置,因物品相同無差別,故物品之間無順序,是組合問題,只有1种放法,根據分步計數原理,共有Cn+m-1 m-1×1=Cn+m-1 m-1種排法
水果分籃問題
例2:有廣西橘子,煙臺蘋果,萊陽梨若干,從中隨意取出四個,問共有多少種不同取法?
問題等價於將四個水果放入三個不同的水果籃,且允許籃子為空,{這裡是逆向思維邏輯}
將4+3=7個水果分為3個組,分組需2個隔板,隔板共有6個放置位置,
故有C(4+2, 2)個選擇,即15種。
物品問題
例3將20個優秀學生名額分給18個班,每班至少1個名額,有多少種不同的分配方法?
分析:本題是名額分配問題,用隔板法.
解析:將20個名額分配給18個班,每班至少1個名額,相當於將20個相同的小球分成18組,每組至少1個,將20個相同的小球分成18組,需要17塊隔板,先將20個小球排成一排,因小球相同,故小球之間無順序,是組合,只有1種排法,再在20個小球之間的19個空檔中,選取17個位置放隔板,因隔板無差別,故隔板之間無序,是組合問題,故隔板有C(19, 17)種不同的放法,根據分步計數原理,共有C(19 ,17)種不同的方法,因17塊隔板將20個小球分成18組,從左到右可以看成每班所得的名額數,每一種隔板與小球的排法對應於一種分法,故有C(n-1, m-1)種分法.
對相同物品分配問題,注意某若干組能否為空,能為空和不能為不空,方法不同,要體會和掌握.