原理
阿貝成像原理認為，透鏡的成像過程可以分成兩步：第一步是通過物的衍射光在透鏡後焦面(即頻譜面)上形成空間頻譜，這是衍射所引起的“分頻”作用；第二步是代表不同空間頻率的各光束在像平面上相干疊加而形成物體的像，這是干涉所引起的“合成”作用。
成像過程的這兩步本質上就是兩次傅立葉變換。如果這兩次傅立葉變換是完全理想的，即信息沒有任何損失，則像和物應完全相似。
如果在頻譜面上設定各種空間濾波器，擋去頻譜某一些空間頻率成份，則將會使像發生變化。空間濾波就是在光學系統的頻譜面上放置各空間濾波器，去掉(或選擇通過)某些空間頻率或者改變它們的振幅和相位，使二維物體像按照要求得到改善。這也是相干光學處理的實質所在。
舉例
以圖l-l為例，平面物體的圖像可由一個二維函式 g(x,y)描述，則其空間頻譜 G(f ， f)即為 g(x ， y)的傅立葉變換：
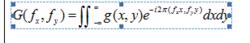阿貝爾二次成像理論設為透鏡後焦面上任一點的位置坐標，則式中為
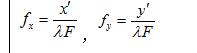阿貝爾二次成像理論方向的空間頻率，量綱為L, F為透鏡焦距，為入射平行光波波長。再進行一次傅立葉變換，將從頻譜分布又還原到空間分布。
為了簡便直觀地說明，假設物是一個一維光柵，光柵常數為，其空間頻率為 f(f=1 /d)。平行光照在光柵上，透射光經衍射分解為沿不同方向傳播的很多束平行光，經過物鏡分別聚焦在後焦面上形成點陣。我們知道這一點陣就是光柵的夫琅和費衍射圖，光軸上一點是0級衍射，其他依次為±1，±2，…級衍射。從傅立葉光學來看，這些光點正好相應於光柵的各傅立葉分量。0級為“直流”分量，這分量在像平面上產生一個均勻的照度。±l級稱為基頻分量，這兩分量產生一個相當於空間頻率為 f餘弦光柵的像。±2級稱為倍頻分量，在像平面上產生一個空間頻率為2 f 的餘弦光柵像，其他依次類推。更高級的傅立葉分量將在像平面上產生更精細的餘弦光柵條紋。因此物鏡後焦面的振幅分布就反映了光柵(物)的空間頻譜，這一後焦面也稱為頻譜面。在成像的第二步驟中，這些代表不同空間頻率的光束在像平面上又重新疊加而形成了像。只要物的所有衍射分量都無阻礙地到達像平面，則像就和物完全一樣。
分析
但一般說來，像和物不可能完全一樣，這是由於透鏡的孔徑是有限的，總有一部分衍射角度較大的高頻信息不能進入到物鏡而被丟棄，所以像的信息總是比物的信息要少一些。高頻信息主要反映物的細節。如果高頻信息受到了孔徑的阻擋而不能到達像平面，則無論顯微鏡有多大的放大倍數，也不可能在像平面上分辨這些細節。這是顯微鏡解析度受到限制的根本原因。特別當物的結構是非常精細(例如很密的光柵)，或物鏡孔徑非常小時，有可能只有0級衍射(空間頻率為0)能通過，則在像平面上雖有光照，但完全不能形成圖像。
波特在1906年把一個細格線作物(相當於正交光柵)，並在透鏡的焦平面上設定一些孔式屏對焦平面上的衍射亮點(即夫琅和費衍射花樣)進行阻擋或允許通過時，得到了許多不同的圖像．設焦平面上坐標為ξ，那么ξ與空間頻率相應關係為
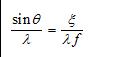阿貝爾二次成像理論(這適用於角度較小時sin θ≈tg θ=ξ/ f， f為焦距)．焦平面中央亮點對應的是物平面上總的亮度(稱為直流分量)，焦平面上離中央亮點較近(遠)的光強反映物平面上頻率較低(高)的光柵調製度(或可見度)．1934年譯尼克在焦平面中央設定一塊面積很小的相移板，使直流分量產生位相變化，從而使生物標本中的透明物質不須染色變成明暗圖像，因而可研究活的細胞，這種顯微鏡稱為相襯顯微鏡。為此他在1993年獲得諾貝爾獎。在20世紀50年代，通信理論中常用的傅立葉變換被引入光學，60年代雷射出現後又提供了相干光源，一種新觀點(傅立葉光學)與新技術(光學信息處理)就此發展起來。
