內容
 阿波羅尼奧斯定理
阿波羅尼奧斯定理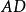 阿波羅尼奧斯定理
阿波羅尼奧斯定理在幾何形狀中, 阿波羅尼奧斯定理表示任何三角形的任意邊的平方和等於第三邊的一半的平方的兩倍,加上第三邊中位數的平方的兩倍 。具體來說,在任何三角形 中,如果 是中線,那么
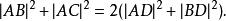 阿波羅尼奧斯定理
阿波羅尼奧斯定理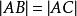 阿波羅尼奧斯定理
阿波羅尼奧斯定理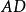 阿波羅尼奧斯定理
阿波羅尼奧斯定理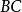 阿波羅尼奧斯定理
阿波羅尼奧斯定理這是一個特殊情況的斯圖爾特定理。對於 的等腰三角形,的中位線垂直於 ,定理簡化為三角形 ADB(或三角形 ADC)的畢達哥拉斯定理。從平行四邊形的對角線相互平分的事實來看,該定理等價於平行四邊形定律 。
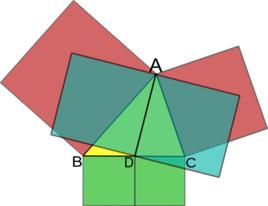
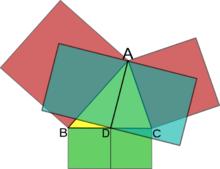 圖1.阿波羅尼奧斯定理
圖1.阿波羅尼奧斯定理證明
該定理可以證明是斯圖爾特定理的一個特例,或者可以用向量證明。以下是使用餘弦定律證明。
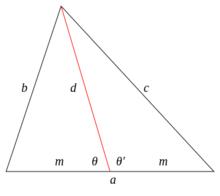 圖2.Apollonius定理的證明
圖2.Apollonius定理的證明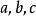 阿波羅尼奧斯定理
阿波羅尼奧斯定理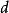 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理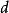 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理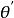 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理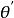 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理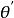 阿波羅尼奧斯定理
阿波羅尼奧斯定理 阿波羅尼奧斯定理
阿波羅尼奧斯定理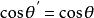 阿波羅尼奧斯定理
阿波羅尼奧斯定理設三角形具有邊 ,其中線 被繪製到 a側。設 是由中線分割 形成的線段長度,因此 是 的一半。設 和 之間形成的角度為 和 ,其中 包括 , 包括 。那么 是 的補充, 。由余弦定理可知:
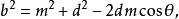 阿波羅尼奧斯定理
阿波羅尼奧斯定理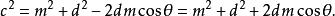 阿波羅尼奧斯定理
阿波羅尼奧斯定理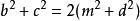 阿波羅尼奧斯定理
阿波羅尼奧斯定理根據這些方程式可得,,即得證。