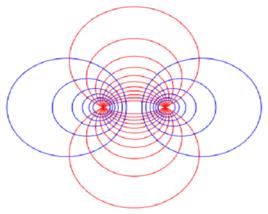
定義
阿波羅尼奧斯圓族是兩個相關的圓族。第一個圓族的每一個藍色圓與第二個圓族的每一個紅色圓相互正交。這些圓構成了雙極坐標系的基。阿波羅尼奧斯圓是希臘數學家阿波羅尼奧斯(古希臘語： Ἀπολλώνιος) 發現的。
阿波羅尼奧斯圓族阿波羅尼奧斯圓是線段定義的，標記此線段為 。
第一族（藍色圓）
阿波羅尼奧斯圓族
阿波羅尼奧斯圓族第一族中的每一個都由一個正實數確定，這些圓定義為滿足下列條件的點的軌跡：
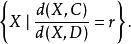阿波羅尼奧斯圓族 阿波羅尼奧斯圓族
阿波羅尼奧斯圓族 阿波羅尼奧斯圓族
阿波羅尼奧斯圓族 阿波羅尼奧斯圓族即到的距離與到的距離之比為.
阿波羅尼奧斯圓族 阿波羅尼奧斯圓族
阿波羅尼奧斯圓族 阿波羅尼奧斯圓族 阿波羅尼奧斯圓族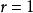
阿波羅尼奧斯圓族
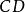阿波羅尼奧斯圓族當很接近零時，相應的圓會靠近的一側，而對接近的, 相應的圓則靠近的一側。至於當時，該圓會退化為線段之中垂線。
第二族（紅色圓）
阿波羅尼奧斯圓族 阿波羅尼奧斯圓族第二族中的每個圓都由角確定， 這些圓定義為滿足下列條件的點的軌跡：
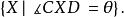阿波羅尼奧斯圓族
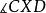阿波羅尼奧斯圓族
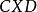阿波羅尼奧斯圓族其中 表示的有向角。
阿波羅尼奧斯圓族
阿波羅尼奧斯圓族 阿波羅尼奧斯圓族 阿波羅尼奧斯圓族當取遍 0 到之所有值時，上式生成所有經過和的圓 。
性質
阿波羅尼奧斯圓族不一樣圓圈的固定比例必不一樣。圓與圓之間互不同心，互不相交。
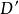阿波羅尼奧斯圓族
阿波羅尼奧斯圓族
阿波羅尼奧斯圓族 阿波羅尼奧斯圓族 阿波羅尼奧斯圓族 阿波羅尼奧斯圓族 阿波羅尼奧斯圓族每一個藍圓與每一個紅圓以直角相交，可以簡易地解釋如下：關於一個圓心為點 的圓 ，一族的藍阿波羅尼奧斯圓的反演像，形成了一組同心圓，其圓心在點 。點關於圓的反演是點。同樣的變換把一族的紅圓反演為一組從點放射出來的直線。這樣，反演將雙極坐標變換為極坐標。在極坐標里，每一條徑向線與 圓心為原點的圓圈 以直角相交。由於反演是一個共形變換，所以，每一個藍圓圈與每一個紅圓圈以直角相交 。
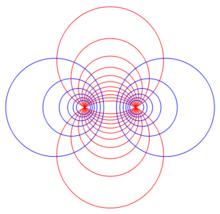圖1 阿波羅尼奧斯圓族