阿基米德三角形

圓錐曲線的弦與過弦的端點的兩條切線所圍成的三角形叫做阿基米德三角形。

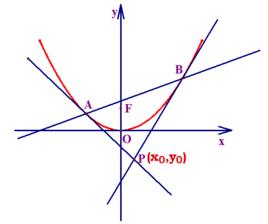
阿基米德三角形過任意拋物線焦點F作拋物線的弦，與拋物線交於A、B兩點，分別過A、B兩點做拋物線的切線l1,l2相交於P點。那么△PAB稱作阿基米德三角形。該三角形滿足以下特性：

1、P點必在拋物線的準線上

2、△PAB為直角三角形，且角P為直角

3、PF⊥AB（即符合射影定理）

另外，對於任意圓錐曲線（橢圓，雙曲線、拋物線）均有如下特性

1、過某一焦點F做弦與曲線交於A、B兩點，分別過A、B兩點做圓錐曲線的切線l1,l2相交於P點。那么，P必在該焦點所對應的準線上。

2、過某準線與X軸的 交點Q做弦與曲線交於A、B兩點，分別過A、B兩點做圓錐曲線的切線l1,l2相交於P點。那么，P必在一條垂直於X軸的直線上，且該直線過對應的焦點。