基本信息
IWO 是一種受野草啟發而提出的、基於種群的數值最佳化計算方法,其執行過程是模擬野草的殖民化過程。作為一種全新的最佳化計算方法, IWO算法具有易於理解、易於編程實現的特點
IWO算法具有柔性的框架,其中的各種機制都可用多種算法予以實現。目前IWO 算法已經在許多領域得到了套用, 譬如標準多維數值最佳化函式集和魯棒控制器最佳化與調節問題、圖像聚類問題、約束工程設計問題、多輸入多輸出 (Multiple Inputs and Multiple Outputs , MIMO)系統天線陣列設計問題、DNA 編碼順序計算問題、壓電激勵器的優 化放置問題、推薦系統問題 、分布數據合併過程進展預測問題以及電力市場動盪性研究問題。
IWO算法是一種新興的計算方法,本文以IWO算法的基本原理為線索,圍繞其構架中的重要機制和參數、算法執行過程和套用領域等方面,對IWO 算法的研究現狀和研究成果進行了全面的綜述,使學者們對IWO 算法有更為廣泛和深入的了解。
野草特性
野草繁殖
野草可以通過細胞以有性或無性方式繁殖。有性繁殖通過種子或孢子形式進行,種子形成後,通過動物、風及水等形式進行空間分散,直到可以找到適合生長的機會空間。在條件成熟時種子進行生長,通過與其他相鄰植物進行相互作用而成長為植株,隨後植株開花結籽。
選擇性進化
在野草的殖民化過程中,相鄰植株會由於生長年限、植株大小和相對距離而相互影響。因此,植物的出生、成長和繁殖 會受到植株密度、種群和植物群的適應性的影響。在植物群 落中,適應性的3個主要因素(繁殖、與競爭者進行生存鬥爭 和躲避天敵)是相互矛盾的。適應性的提高可以使植物能夠生存更長時間,而對於植物適應性的估計必須考慮以上3個因素。植物的自然進化選擇方式有多種,其中有兩種選擇方式比較重要,分別是r選擇和K選擇。r選擇是要從植物群 中選擇出能夠長得快、繁殖快和消亡快的植物並讓這些植物去占據不穩定的和不可預測的環境,K選擇是要從植物群中選擇出能夠長得慢、繁殖慢和消亡慢的具有很強的競爭性的植物去占據一個具有高競爭壓力、資源有限、穩定的和可預測的環境。r選擇對應於IWO算法的全局探索方式,K選 擇對應於IWO算法的局部搜尋方式。
野草算法
野草算法的執行過程要經歷4個步驟:(1)初始化種群; (2)繁殖;(3)空間分布;(4)競爭性生存。
初始化種群
在這個步驟中,需要確定種群P(種群是族群的一部分)和族群Q的大小P size和Q size、最大疊代次數iter max、問題維數d、最大和最小可生成種子數S max和S min 、非線性指數n、區間步長初始值σinit和最終值σfinal以及初始搜尋空間X,並隨機生成P size個解。
繁殖
種群中的成員能夠散播的種子數是根據該成員的適應值及族群所有個體的最低和最高適應值來決定的,圖1描述了種子數的確定過程。在用最佳化算法求解問題的過程中,我們可能會直覺地認為可行解比不可行解具有更好的適應值,因此會放棄不可行解。然而,這種做法忽視了進化算法具有機率性,其產生的解是在不可行和可行之間不斷轉化的。在進化過程中,不可行解可能比可行解帶有更多有用信息。在IWO算法中,繁殖過程按照自然界中的繁殖法則,給予不可行的個體生存和繁殖的機會,只是這種機會相對較少。
空間分布
野草族群的種子數確定方法IWO算法種群產生的種子被隨機播撒在d維空間中,產生種子的方式是通過將某個解加上 某個數值 D,而該數值的變化區間步長的大小是由σ來決定的(也就是說 D∈[-σ, σ])。 如果用 σinit ,σfinal ,σcur ,itermax ,iter 以及n分別表示最初的區間步長、最終的區間步長、當前的區間步長、最大疊代次數、當前疊代數以及非線性調節指數,則它們之間的關係為
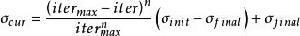野草算法式(1)確保了在較遠區域進行播種的機率在以非線性的方式逐漸降低,這樣會使適應值好的個體聚集在一起而一些不適應的個體被清除,這恰好對應了野草進化過程中從r選 擇方式到K選擇方式的過渡。
競爭性生存法則
如果一種植物沒有後代,它將滅亡;如果一種植物不斷產生後代,這一植物種類將占據整個世界。因此,有必要在植物族群中通過控制族群大小來保持各種植株類型間的競爭性。在進行了一定的疊代之後,植物族群會因快速的繁殖而達到它的最大允許數量。然而,我們希望適應性強的那些植株能 夠比適應性差的植株多。因此採用競爭性生存法則,其執行方式為:當族群中的野草數量達到最大值時,每個植株都按照前面的方式進行繁殖和空間分布。隨後,這些新產生的後代與族群中的植株按照適應值大小進行排序,排序後的植株按適應值從大到小選擇出 Qsize個植株,其餘的植株被清除(也就是說從這以後,算法的種群大小就保持為 Qsize 個)。這種機制給予那些適應值低的個體繁殖的機會,如果它們的後代的適應值更好,這些後代就可以生存下來。這種先讓植株進行快速的繁殖和生長來適應環境,之後再保留一些在相對穩定的環境下更具有競爭力的個體繼續探索環境的方式,也可以認為是模擬了生物的r選擇和K選擇方式。
算法執行步驟
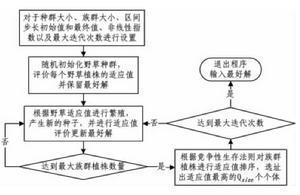IWO算法步驟Step 1 種群初始化(包括參數的設定和初始解(植株)的生成和評價);
Step 2 對於每個解,根據圖1確定允許的後代個數 ;
Step 3 根據式(1)的限定,在解的每一維上進行加減某個數值D的操作來產生新的解並評價這些新的解;
Step 4 如果現有解的數量小於Qsize ,則執行Step 2,否則轉Step 5 ;
Step 5 根據競爭性生存法則選取Qsize個適應值最好的解;
Step 6 如果iter < itermax ,則轉Step 2,否則退出算法執行過程並輸出最優解。
圖2顯示了IWO算法的執行步驟邏輯關係。
IWO算法的相關研究
目前,IWO算法已經廣泛套用於許多自然科學與工程科 學領域,並顯示出強大的優勢和潛力。
多維數值最佳化函式集和魯棒控制器最佳化與調節問題
2006年,Mehrabian和Lucas通過IWO算法求解3個標準多維數值最佳化函式集和1個魯棒控制器最佳化與調節問題,將各種算法參數組合進行了系統的測試。通過與遺傳算法、元算法和粒子群算法、隨機蛙跳算法及多個版本的模擬退火算法進行計算結果比較,表明對於所有問題IWO算法都獲得了令人滿意的結果,IWO算法比其他算法的結果更好。對於參數選擇方面的建議,種群數P為10至20之間、非線性指 數n為3、最大和最小可生成種子數為2和0。關於其餘的參數如何選 取問題,Mehrabian和Lucas沒有直接給出答案。
圖像聚類問題
2008年,蘇守寶等將IWO算法用於求解圖像聚類問題。在該文中,採用最小量差、最小簇內距離以及最大簇間距離作為目標,通過構造除法的形式將多目標問題轉化為單目標問題。採用IWO算法對圖像數據集的簇中心進行準確定位,動態確定圖像聚類簇數的最優選擇範圍。通過幾個基準測試圖像,將IWO算法測試結果與K-均值、FCM和粒子群最佳化算法的結果進行了比較,表明IWO算法具有更穩定的圖 像聚類性能,IWO算法能夠獲得更好的圖像聚類效果
約束工程設計問題
2009年,蘇守寶等將IWO 算法用於求解約束工程設計問題,結合罰函式法將IWO 算法套用於求解壓力彈簧和焊 接束最佳化問題。通過將IWO算法的求解結果與粒子群算法 (PSO)、遺傳算法(GA)和蟻群算法(ACO)的求解結果進行比較,表明IWO算法獲得了更優的結果,體現了算法的全局尋優能力。通過實驗與統計分析,顯示IWO算法求解問題時的 部分最佳參數:n為3、初始種群大小為20至30之間並且算 法最大疊代次數是500。但是該文存在一點疑問,在參數設定時族群大小Qsize 為10,而初始種群大小為20。這與IWO算法的執行原理相違背,因為只有在族群大於等於初始種群時,種群中的解才有可能進行繁殖,也就是說族群大小不可能小於初始種群大小。
MIMO 系統天線陣列設計問題
MIMO天線系統是第四代移動通訊系統,是能夠滿足大 量數據傳輸的高速、高質量的傳輸系統。在很小的終端設備 上採用 MIMO技術會導致天線單元之間的高耦合性和空間 信號干擾,從而影響 MIMO信道的傳輸能力。有效地設計MIMO系統天線陣列,可以有效減少接收信號的相互干擾。
2008年,Mallahzadeh等採用IWO算法求解了4個天線設定問題,將 求解的結果與PSO算法的結果進行了比較,結果表明IWO算法的正確率和收斂速度都優於PSO算法。2009年,Mallahzadeh等採用IWO算法 求解了2部件和4部件E型MIMO貼片天線陣列正交集安排問題,旨在降低天線陣列的耦合性結果表明,IWO算法能夠有效地獲取天線陣列的 最優設計方案。2009年,Mallahzadeh等採用IWO算法求解了小型U型 MIMO天線陣列設計問題。首先, IWO算法被用於求解單個U型MIM O天線設計問題;在獲得有用參數後,IWO算法被用於求解2部件和4部件貼片天線陣列設計問題。求解結果表明,IWO算法的設計方案能夠有效降低天線間的耦合性,提高了信號的信道頻寬。2009年,Pal等人採用IWO算法求解了線性天線陣列設計問題。通過與遺傳算法、粒子群算法、元算法(MA)和禁忌搜尋算法(TS)的求解結果進行比較,表明IWO算法的目標函式平均值和解標準差都好於其他算法的對應值。
推薦系統問題
推薦系統可幫助客戶從大量商品中找到他們感興趣的商品。為了使客戶能夠得到更具個性化的推薦,需要根據每個客戶分配優先權。通過採用最佳化算法,可以確定每個客戶的最佳優先權。2007年,Rad和Lucas採用IWO算法求解了推薦系統最佳優先權分配問題。採用一個電影數據集,將IWO算法的求解結果與遺傳算法和粒子群算法的求解結果進行了比較,結果表明IWO算法的結果更準確。
壓電激勵器的最佳化放置問題
Mehrabian 和 Yousefi-Koma分別於2007年和2009年在兩個不同的雜誌上發表了關於採用IWO算法解決飛機尾鰭上的壓電激勵器的最佳化放置問題。問題的解由二維變數表示,代表平面上的一個點。從計算結果來看,IWO算法能夠準確地定位激勵器並且有效地削減了激勵器的震動。
分布數據合併過程進展預測問題
2008 年,Kostrzewa和Josinski採用IWO算法求解了分散數據合併過程進展預測問題,並將求解結果與一個自適應進化算法的結果進行了比較。問題採用基因串表達形式, 每個基因由一個三元組(Si,Sj,Wk)組成,這裡Si和Sj表示要進行合併的兩個數據,Wk表示第k個工作站。從計算結果看,IWO算法的計算時間較長,但最好解的質量優於自適應 算法。
