簡介
重要性採樣是蒙特卡洛方法中的一個重要策略。該方法不改變統計量,只改變機率分布,可以用來降低方差 。
重要性採樣算法就是在有限的採樣次數內,儘量讓採樣點覆蓋對積分貢獻很大的點。
目標
其目標是用一種受控的方式改變仿真,以便增加稀少事件的數目,同時還能正確地確定解調差錯機率。常規重要性採樣(CIS)是一種降方差的仿真方法,它通過提供有偏噪聲來實現,等效於使系統工作在一個較低的信噪比環境下。
原理
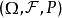 重要性採樣
重要性採樣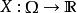 重要性採樣
重要性採樣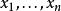 重要性採樣
重要性採樣假設為機率空間上的一個隨機變數。我們想要估計 X的期望值,記作 E[ X;P]。如果根據 P隨機抽取樣本,估計的期望值即
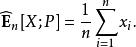 重要性採樣
重要性採樣這一估計的精確度取決於 X的方差,
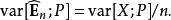 重要性採樣
重要性採樣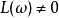 重要性採樣
重要性採樣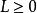 重要性採樣
重要性採樣而重要性採樣的基本思想則是從另一個分布中抽取樣本,用以降低 E[ X;P]估計的方差。進行重要性採樣時,首先選擇一個隨機變數,使得 E [L;P]=1,並滿足 P上幾乎處處。由此,可以定義新的機率
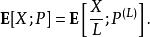 重要性採樣
重要性採樣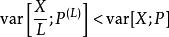 重要性採樣
重要性採樣於是,我們可以從 P上抽樣,通過變數 X/L估計 E[ X;P]。如果成立,此時的估計便優於直接在原分布上採樣得到的估計。
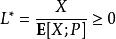 重要性採樣
重要性採樣當 X在Ω上不變號時,最優的 L為。此時 X/L*即為要估計的 E[ X;P],只需一個樣本便可得到該值。然而由於 L*與要估計的 E[ X;P]有關,在實際操作中我們無法取到理論上最優的 L*。不過,我們仍可以採用如下方式逼近該理論值:
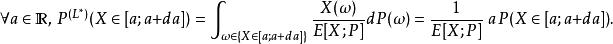 重要性採樣
重要性採樣於是,要估計的期望值可改寫為:
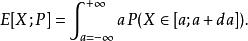 重要性採樣
重要性採樣注意到,更優(即讓估計值方差更小)的 P會使得樣本分布的頻率與其在 E[ X;P]計算中的權重更加相關。這也是該方法得名“重要性採樣”的原因。
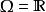 重要性採樣
重要性採樣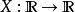 重要性採樣
重要性採樣重要性採樣常用於蒙特卡洛積分。當P為均勻分布、時, E[ X;P]即為實函式的積分。

