重心重分

重心重分是復形的一種特殊的重分。可歸納地定義復形 K 的第 m 次重心重分復形。復形經過重心重分後雖然單形變小了，但單形大小的變化有一定規律。

簡介

重心重分是復形的一種特殊的重分。單形的重心用 s 表示，復形 K 的重心重分是按下面方式定義的復形SdK:

重心重分

1. Sd K的頂點集

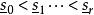重心重分

重心重分

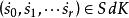重心重分

2.若是 K 的單形的一個真面序列，則，並稱一為這單形的主導頂點。

這樣得到的Sd K為一個復形，|Sd K|=|K|，dimSd K=dim K。

第m次重心重分復形

可歸納地定義復形 K 的第 m 次重心重分復形。

重心重分

復形經過重心重分後雖然單形變小了，但單形大小的變化有一定規律。首先單形的直徑

重心重分

變小了；其次，若 K 為 n 維復形，復形的網徑指復形中各個單形直徑的最大值，即是網徑

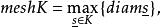重心重分

則

重心重分

從而當 m 充分大時，Sd K 的網徑可任意小，即

重心重分