基本介紹
極圓
極圓 極圓
極圓給定一個鈍角三角形，極圓是以垂心H為圓心， 為半徑的一個圓， 的平方由下式給出(式中 是三角形三邊上的垂足)
極圓
極圓
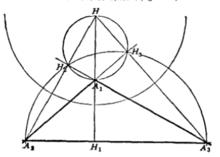圖1極圓是德朗香圓的反補。極圓與斯坦納內切橢圓的準圓、第二杜洛斯一凡利圓和斯蒂范維卡圓正交 。
相關結論
僅在三角形有一個鈍角時，才有實的極圓存在，對鈍角三角形，我們可以立即建立如下的定理：
定理1關於極圓，三角形的每個頂點與從它所引出的高在對邊的垂足，互為反演點；每條邊是所對頂點的極線。一條邊的反形是一個圓，以所對的頂點到垂心的連線為直徑。以三角形任一邊為直徑的圓，經過這個反演不變，因此與極圓正交。更一般地，通過一個頂點及這點所引出的高的垂足的圓，即以從頂點引到對邊的線段為直徑的圓，經過這個反演不變，並與極圓正交。外接圓關於這個極圓的反形是九點圓 。
定理2 三角形關於它的極圓是自共軛的；反過來，一個圓是自共軛三角形的極圓。
極圓
極圓
極圓在一個垂心組中，組成的四個三角形有三個是鈍角三角形；例如設是一個鈍角三角形，H是它的垂心，則三角形有實的極圓，圓心分別在。
定理3一個垂心組的任意兩個極圓正交。
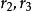極圓因為設為兩個極圓的半徑，它們的圓心分別為A，A，則
極圓
極圓這就是正交的條件.
定理4 任意兩個極圓的根軸是第三個頂點引出的高。
暫且承認“虛圓”的存在；這樣的圓有一個實的圓心，而半徑的平方是負值，於是，如上面所說，一個垂心組的三角形有四個極圓，三個實的，一個虛的，四個中任兩個正交，反過來，如果四個圓互相正交，它們的圓心是一個垂心組，除非是將要提到的退化情形，一個關於這種組的有趣的定理是：
定理5設依次地關於四個互相正交的圓的每一個施行反演，則每一個點回到原來的位置。
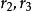極圓
極圓因為設我們將這圖形簡化，使這四個圓中的兩個變為互相垂直的直線，這時可以看到另兩個是以這兩條直線的交點為圓心的同心圓，半徑是,而。對這個特殊圖形，定理容易證明，因此它對一般圖形也成立。
考慮由四條直線，每兩條不互相垂直，確定的三角形的極圓。我們看到其中至少有兩個是鈍角三角形，四個也可以全是鈍角的，考慮其中一個，如A'B'C'，在它的各邊上有三個共線的點A,B,C，我們已經看到A'B'C'的極圓與以AA', BB' ,CC'為直徑的圓正交。
定理6 完全四邊形的各個三角形的極圓，組成共軸圓組，與以對角線為直徑的圓共軛 。
