選址模型
正文
用於求解最優選址問題的運籌學模型。最優選址問題是指：已知若干現有設施的地址，確定一個或幾個新設施的地址。這裡設施的含意是廣義的，可以指提供服務的設施，也可以指需要服務的設施。最優選址問題的典型例子有:已知工廠和用戶的位置,確定新倉庫的最優地址；已知供電區域，選擇發電廠的最優地址；已知一組油井的位置，確定煉油廠的最優地址；已知讀者服務區域，選擇圖書館的最優地址等。最優選址問題分單源選址問題和多源選址問題。單源選址問題是已知若干個現有設施，選擇一個新設施的最優地址。多源選址問題則是已知若干個現有設施，選擇兩個或多個新設施的最優地址。多源選址問題還要確定哪個新設施應為哪些現有設施服務，或哪些現有設施應為哪個新設施服務。這裡包含著分配問題，所以又稱為選址－分配問題。選址問題還可以分為連續型選址問題和離散型選址問題。連續型選址問題是假定待選區域中任一點的地位均與其他點的地位相同，因而在數學上就有無限多個可能的地點存在。離散型選址問題則是假定待選區域內只有有限多個事先已經知道的位置。單源連續型選址問題 設(xj，yj)是需要供應或服務的已知點在平面上的坐標,(x，y)是待求的源的坐標；cj是單位貨物傳送單位距離的運價；bj是各需求點對貨物的需求量(j=1,2,…,n)。從(x，y)到任一需求點(xj，yj)的運費是bjcj【(x-xj)2＋(y-yj)2】1/2,如令dj＝【(x-xj)2+(y-yj)2】1/2,則運費為bjcjdj。因此,從(x，y)到所有需求點的總運費
。求此函式關於x和y的偏導數,並使其等於0，即可求得它的極小值。即 
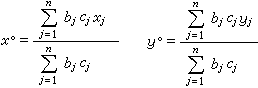
多源連續型選址問題 多源選址問題的一般提法是：已知各個終點的位置和需求量以及該區域內的運價，求源的個數、各個源的位置、如何將終點劃分給各個源和各個源的容量。為了使問題簡化，通常假定各個源許可的容量不受限制，單位運價與源的總輸出量無關。多源連續型選址問題比較複雜，現有兩種適用於大型多源選址問題的近似解法：交替選址-分配法和隨機終點法。
交替選址-分配法 交替選址-分配法是一種單調下降的收斂過程。它的基本步驟是:①將n個終點組成的集合劃分成元素個數大致相等的子集。②對 m個子集中的每一個子集求解單源選址問題。③檢查每一個終點，如果它離②中求出的某一個源比分配給它的那個源靠得更近，則重新分配各終點。④如果要重新分配，則回到②，否則計算即可終止。
隨機終點法 它的基本步驟是：①根據1到n各個整數的均勻分布產生m個隨機數。這裡n是終點數,m是源數。②將標號為這m個整數的終點看作源，而把其餘n-m個終點分配給費用最小的源。設(xs，ys)是所考慮的源,分配時應使 bjcj【(xs-xj)2+(ys-yj)2】1/2取極小值。③重複①和②，直到滿足終止準則為止，每次重複均保留費用最小的解。④求解m個單源選址問題,看結果有無改進,以求得最優解。根據一個事先確定的數或行之有效的簡單方法即可終止這種隨機地產生嘗試解的求解過程。
參考書目
L.庫珀等著，魏國華等譯：《運籌學模型概論》，上海科學技術出版社，上海，1987。(L.Cooper,U.N.Bhat,L.J.LeBlanc，Introduction to Operations Research Models，W.B. Saunders Comp.，Philadelphia，London, Toronto, 1977.)
