簡介
哈夫曼編碼(Huffman Coding)，又稱霍夫曼編碼，是一種編碼方式，哈夫曼編碼是可變字長編碼(VLC)的一種。Huffman於1952年提出一種編碼方法，該方法完全依據字元出現機率來構造異字頭的平均長度最短的碼字，有時稱之為最佳編碼.
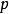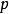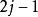適應性哈夫曼編碼 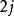適應性哈夫曼編碼
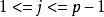適應性哈夫曼編碼
適應性哈夫曼編碼
適應性哈夫曼編碼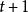
適應性哈夫曼編碼
適應性哈夫曼編碼 適應性哈夫曼編碼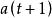
適應性哈夫曼編碼 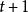適應性哈夫曼編碼 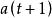適應性哈夫曼編碼 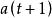適應性哈夫曼編碼 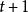適應性哈夫曼編碼適應性哈夫曼編碼是基於哈夫曼編碼的特點實現的，哈夫曼樹必須具有如下的屬性（假設有 個葉子結點）： 個葉子結點，每個葉子結點的重量都是非負的，並且某個內部結點的重量是其兒子結點重量之和。結點的順序按照每個結點的重量升序排列，因此第 個結點和第 個結點是兄弟結點。 ；某個結點的父結點的結點號一定大於此結點的結點號。動態哈夫曼編碼的關鍵是如何將前 個字元的哈夫曼樹調整成一顆前 個字元的哈夫曼樹。為解決上述問題，需分兩步走，第一步把 個字元的哈夫曼樹轉換成它的另一種形式，在該樹中只需在第二步中簡單的把有根到 路徑上所有結點的重量加1，就可以變成前 個字元的哈夫曼樹，其過程就是以葉結點 為當前結點，重複的將當前結點與具有同樣重量序號最大的節點進行交換，並使後者的父結點成為當前結點，直到遇到根結點為止，第一步通過將根到葉結點 路徑上的所有結點重量加1，就變成了前 個字元的哈夫曼樹。
兄弟性質
在哈夫曼編碼中，有個缺點是除了壓縮後的資料外，它還得傳送機率表給解碼端，否則解碼端無法正確地做解碼的工作。如果想要壓縮好一點，必須有更多的統計資料，但同時必須要送出更多的統計資料到解壓縮端。而適應性編碼可以利用已經讀過的資料機動的調整哈夫曼樹。適應性哈夫曼編碼中，算法FGK的基本原則是根據兄弟性質（Sibling Property），由Gallager定義。一顆哈夫曼樹只是一棵在每個節點，包括樹葉與內節點，加上加權值得二叉樹，除了樹根外，每一個節點都有一個兄弟節點與其共有一個父親節點。如果每一個節點可以按照加權值從小排列到大且每個節點又再自己的兄弟相鄰，稱為兄弟性質。修改、或更新一棵哈夫曼樹包括兩個步驟。第一個步驟是頻率次數的增加，先找到該葉子，把頻率加一，在往上找他的父親節點，也跟著加一，直到樹根皆照著此步驟。第二個步驟是如果增加加權值的動作使得兄弟性質不再滿足時，必須做調整的動作，藉由交換葉子改變頻率增加的順序，同時，交換位置後的父親節點加權值也要跟著更新，以此原則使之再度成為哈夫曼樹。
有關算法
FGK算法
在算法FGK中，傳輸端與接收端同時動態的去改變哈夫曼樹，最初，解碼樹由單一葉子組成，稱之0端。0端是用來代表未出現過的訊息，當每一個訊息傳遞後，增加此訊息的出現頻率並調整哈夫曼樹保持兄弟性質。當有t個訊息傳遞後，之中有k個不同的訊息，代表此哈夫曼樹有k+1的葉子，k個葉子有訊息，1個代表0端。當下次傳遞新訊息時，此訊息夾帶未出現過的資訊，0端的葉子此時分成2片葉子，1片給新訊息，另一片為新的0端。
考慮適應性哈夫曼編碼的效能問題，更有效能的方法是確認編碼端不會浪費空間在不存在的符號上，一般的哈夫曼編碼容易做到是因為在建立哈夫曼樹之前，會統計所有的資料，就能先算出各訊息的頻率；相反的，適應性編碼不一樣，並不知資料出現的頻率，因此假設所有訊息長度都一樣是log_2q個位元，伴隨著統計資料的增加，訊息的編碼長度會愈來愈短。但此方法有個缺點，在大部分情況會浪費許多空間，尤其在短訊息的情況，大部分未使用的符號會改變整個統計表，使得壓縮結果大打折扣。
舉例來說，符號源有256個符號，一開始的哈夫曼樹就有這256個符號，且加權值設為1，即使連續讀進16個e，也仍然需要四個位元以上來編碼e，因為其他沒出現的255個符號使得哈夫曼樹的調整速度變慢。
解決的方法可以一開始統計表都沒有東西，當訊息被讀進去時在加入到統計表內，假設一開始哈夫曼樹只有兩個符號，兩個符號加權值都是一，且都不改變，一個代表檔案結束，另一個符號較特別，如果辨識的符號，哈夫曼樹已經有了，就像上述正常的操作，如果哈夫曼樹沒出現過，先送出此符號，再送出此符號的ASCⅡ碼，最後將這個加入哈夫曼樹，設定加權值為1，調整哈夫曼樹。這種方法，如過訊息是連續16個e，除了第一個e是九個位元，後面的所有15個e都只需要一個位元表示。
Vitter算法
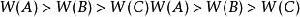適應性哈夫曼編碼編碼一樣是用樹狀結構表示，每個支點都有對應的權重及特定數字，數字從上到下、從左到右排列，權重要遵守兄弟性質，如果A是B的父親且B是C的父親，則 。
權重用來計算支點編碼及其小孩（底下的支點）的數量，一樣權重的胝點會形成一個區塊，要得到每個支點的編碼，在二進制樹上，傳輸所有從樹根到此支點的路徑，往右走就寫1，往左走就寫0。需要有系統且簡單的方式去表示還沒傳遞（NYT），可以使用字母去傳遞二進制數字，編碼跟解碼都是從一個有最大數字的樹根開始，當傳遞NYT時，必須傳遞編碼到NYT支點，接著是普遍的支點，當每一個符號都完成後，只要傳遞編碼到自己的葉子支點即可。
