詳解
在熱力學中，明確定義的量以描述通過熱力學系統的平衡狀態空間的過程的路徑被稱為 過程函式，或者可選地， 過程量或 路徑函式。 例如，機械功和熱是過程功能，因為它們定量地描述了熱力學系統的平衡狀態之間的過渡。
路徑函式取決於從另一個狀態到達一個狀態所採用的路徑。不同的路線給出不同的數量路徑功能的示例包括工作，加熱和弧長。與路徑功能相反，狀態函式與所採用的路徑無關。熱力學狀態變數是點函式，與路徑函式不同。對於給定狀態，被視為一個點，每個狀態變數和狀態函式都有一個確定的值。
過程函式
過程函式 過程函式 過程函式過程函式 X的無窮小變化通常表示為將它們與寫入的狀態函式 Y中的無窮小變化區分開來。數量是一個精確的差異，而不是，這是一個不精確的差別。可以集成過程函式的無窮小變化，但兩個狀態之間的積分取決於兩個狀態之間的特定路徑，而狀態函式的積分只是兩個點處的狀態函式的差異，與採取的路徑。
過程函式
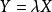過程函式 過程函式
過程函式
過程函式
過程函式
過程函式
過程函式通常，過程函式 X可以是完整的或非完整的。對於 完整過程函式，輔助狀態函式（或積分因子可以定義為這樣是一個國家職能。對於非完整過程函式，不能定義這樣的函式。換句話說，對於完整過程功能， 可以定義為這樣是一個確切的差異。例如，熱力學工作是積分因子以來的完整過程函式 （其中p是壓力）將產生體積狀態函式的精確差異。在熱力學第二定律，通過規定右端是Carathéodory基本上相當於熱量是因為積分因子一期完整的過程函式的聲明（其中T是溫度）將產生熵狀態函式的精確差分。
