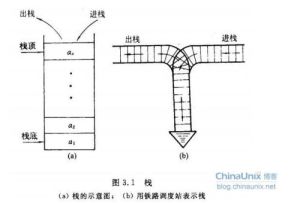
簡介
進棧:多用於計算機,與其相對應的是出棧;進棧、出棧多是按照一定順序的。
例如:有一個數列(23,45,3,7,3,945)
我們先對其進行進棧操作,則進棧順序為:23,45,3,7,3,945
我們在對其進行出棧操作,則出棧順序為:945,3,7,3,45,23
為了方便,我們通常做到:出棧後不再進棧。
進棧出棧就像只有一個口的長筒,先把數據一個個放入筒內,而拿出的時候只有先拿走上邊的,才能拿走下邊的。
棧的套用
棧的典型套用有算術表達式的檢查和背包問題等,實際上,凡屬符合後進先出原則的問題,都可以用棧來處理。
1、算術表達式中括弧作用域合法性的檢查
括弧作用域的檢查是棧的典型實例。檢查一個算術表達式中使用的括弧是否正確,應從下面兩個方面考慮:
(1)左右括弧的數目應該相等;
(2)每一個左括弧都一定有一個右括弧與之匹配。
算法思想:括弧作用域檢查的原則是,對表達式從左到右掃描。當遇到左括弧時,左括弧入棧;當遇到右括弧時,首先將棧頂元素彈出棧,再比較彈出元素是否與右括弧匹配,若匹配,則操作繼續;否則,查出錯誤,並停止操作。當表達式全部掃描完畢,若棧為空,說明括弧作用域嵌套正確,反之,說明表達式有錯誤。
2、背包問題
問題:假設有n件質量分配為w1,w2,...,wn的物品和一個最多能裝載總質量為T的背包,能否從這n件物品中選擇若干件物品裝入背包,使得被選物品的總質量恰好等於背包所能裝載的最大質量,即wi1+wi2+...+wik=T。若能,則背包問題有解,否則無解。
算法思想:首先將n件物品排成一列,依次選取;若裝入某件物品後,背包內物品的總質量不超過背包最大裝載質量時,則裝入(進棧);否則放棄這件物品的選擇,選擇下一件物品試探,直至裝入的物品總和正好是背包的最大轉載質量為止。這時我們稱背包裝滿。
若裝入若干物品的背包沒有滿,而且又無其他物品可以選入背包,說明已裝入背包的物品中有不合格者,需從背包中取出最後裝入的物品(退棧),然後在未裝入的物品中挑選,重複此過程,直至裝滿背包(有解),或無物品可選(無解)為止。
具體實現:設用數組weight[1..N],stack[1,N]分別存放物品重量和已經裝入背包(棧)的物品序號,MaxW表示背包的最大裝載量。每進棧一個物品,就從MaxW中減去該物品的質量,設i為待選物品序號,若MaxW-weight[i]>=0,則該物品可選;若MaxW-weight[i] < 0,則該物品不可選,且若i>n,則需退棧,若此時棧空,則說明無解。
用Pascal實現的參考函式:
Function knapstack(n,MaxW,weight);
begin
top:=0; i:=1; {i為待選物品序號}
while (MaxW>0) and ( i < = n ) do
begin
if (MaxW-weight[i]>=0) and ( i < = n ) then
begin top:=top+1; stack[top]:=i;MaxW=MaxW-weight[i] end;
{第i件物品裝入背包}
if MaxW=0 then return(true)
else begin
if (i=n) and (top>0) then {背包內有不合適物品}
begin {取棧頂物品,恢復MaxW的值}
i:=stack[top]; top:=top-1;MaxW=MaxW+weight[i];
if top>0 then begin
i:=stack[top]; top:=top-1;MaxW=MaxW+weight[i];
end;
end;
i:=i+1;
end;
end;
return(false) {問題無解}
end;