簡介
通解結構定理(structure theorem of general solution)，是關於線性常微分方程解的結構性質的數學表述。
設n階非齊次線性微分方程
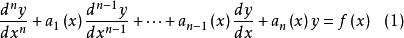通解結構定理
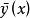通解結構定理
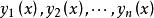通解結構定理的一個特解為 ，與(1)對應的齊次微分方程的n個解為 ；
非齊次線性線性微分方程組
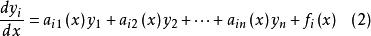通解結構定理 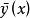通解結構定理 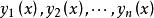通解結構定理(i=1,2,…,n)的一個特解也用 表示，與(2)對應的齊次微分方程組的n個解也用 表示。
齊次方程通解結構定理
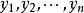通解結構定理 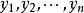通解結構定理這時， 均為向量函式(參見“線性微分方程組”條目)，則關於齊次微分方程(組)的通解結構定理為：如果 是齊次方程(組)的一個基本解組，則
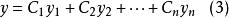通解結構定理
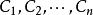通解結構定理包含了方程(組)的所有解，其中 為n個任意常數。顯然，解組(3)表示了方程(組)的通解。
非齊次方程通解結構定理
關於非齊次微分方程(組)的通解結構定理為：非齊次微分方程(組)的通解等於它的對應的齊次方程(組)的通解與它本身的一個特解之和，即
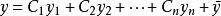通解結構定理常微分方程發展歷史
常微分方程理論的形成與發展是與力學、天文學、物理學及其他自然科學和技術的發展密切相關並彼此促進和推動的。數學的其他分支的新發展，如代數、函式論、李群、拓撲學等都給常微分的發展以深刻的影響。目前計算機科學的高速發展，為常微分方程理論與套用的發展，也提供了很重要的條件。
早在18世紀，常微分方程發展的古典時期，由於力學、物理學、幾何學等的需要，數學家曾吧注意力主要集中在求可用初等函式表示的通解上。在這個階段，主要有萊布尼茨（Leibniz，G.W.）約翰第一·伯努利（Bernoulli，Johann，I）和歐拉（Euler，L.）等人的工作。他們得到了關於其次方程、線性方程和伯努利方程的通解求法。但後來人們發現，絕大多數微分方程都求不出通解，特別是劉維爾（Liouville，J.）於1841年證明了黎卡提方程在除了某些m的特殊值外，其通解不可能用初等函式和初等函式的積分表示。當然，對於一般的非線性方程更是如此。這樣人們開始改變了原來的想法，不局限於求用初等函式表示的解，而去求它的近似解或者去研究滿足這些條件的解的性質。近代電子計算機出現以後，微分方程數值解法發展成近代計算數學中的一個重要分支。
19世紀中葉以後，數學分析理論發生了重要的飛躍，在這個時期，柯西（Cauchy，A.L.）等人建立了嚴格的數學分析的基礎，將新的概念和方法套用於常微分方程，並由實數域擴展到複數域進行研究，嚴格地建立了解的存在惟一性理論，為常微分方程理論的深入研究奠定了堅實的基礎。這個時期柯西等數學家研究了對特定初始值求相應解的問題。這類定解問題稱為微分方程的柯西問題，通稱初值問題。這個時期，由於熱傳導和弦振動等數理方程的定解問題，因而就出現了由斯圖姆（Sturm，J.C.F）和劉維爾等開創的微分方程邊值問題與特徵值問題的研究領域。
