簡介
逐步回歸是一種線性回歸模型自變數選擇方法，其基本思想是將變數一個一個引入，引入的條件是其偏回歸平方和經驗是顯著的。同時，每引入一個新變數後，對已入選回歸模型的老變數逐個進行檢驗，將經檢驗認為不顯著的變數刪除，以保證所得自變數子集中每一個變數都是顯著的。此過程經過若干步直到不能再引入新變數為止。這時回歸模型中所有變數對因變數都是顯著的。
逐步型選元法
逐步回歸法選擇變數的過程包含兩個基本步驟：一是從回歸模型中剔出經檢驗不顯著的變數，二是引入新變數到回歸模型中，常用的逐步型選元法有向前法和向後法。
向前法：向前法的思想是變數由少到多，每次增加一個，直至沒有可引入的變數為止。具體步驟如下。
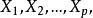逐步回歸步驟1:對 p 個回歸自變數 分別同因變數 Y 建立一元回歸模型
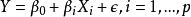逐步回歸
逐步回歸
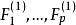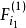逐步回歸
逐步回歸計算變數 ，相應的回歸係數的 F 檢驗統計量的值，記為 ,取其中的最大值 ，即
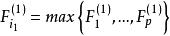逐步回歸
逐步回歸
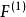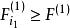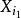逐步回歸
逐步回歸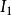
逐步回歸
逐步回歸對給定的顯著性水平 ，記相應的臨界值為 ， ，則將 引入回歸模型，記 為選入變數指標集合。
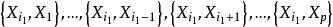逐步回歸
逐步回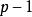歸
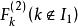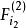逐步回歸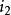
逐步回歸
逐步回歸步驟2:建立因變數 Y 與自變數子集 的二元回歸模型（即此回歸模型的回歸元為二元的），共有 個。計算變數的回歸係數 F 檢驗的統計量值，記為 ，選其中最大者，記為 ,對應自變數腳標記為 ，即
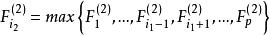逐步回歸。
逐步回歸
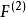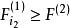逐步回歸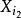
逐步回歸
逐步回歸對給定的顯著性水平 ，記相應的臨界值為 ， 則變數 引入回歸模型。否則，終止變數引入過程。
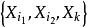逐步回歸步驟3:考慮因變數對變數子集 的回歸重複步驟2。
依此方法重複進行，每次從未引入回歸模型的自變數中選取一個，知道經檢驗沒有變數引入為止。
向後法與向前法正好相反，它事先將全部自變數選入回歸模型，任何逐個剔除對殘差平方和貢獻較小的自變數。
實施過程
逐步回歸分析的實施過程是每一步都要對已引入回歸方程的變數計算其偏回歸平方和（即貢獻），然後選一個偏回歸平方和最小的變數，在預先給定的水平下進行顯著性檢驗，若顯著則該變數不必從回歸方程中剔除，這時方程中其他幾個變數也都不需要剔除（因為其他幾個變數的偏回歸平方和都大於最小的一個更不需要剔除）。相反，如果不顯著，則該變數需要剔除，然後按偏回歸平方和由小到大地依次對方程中其他變數進行檢驗。將對影響不顯著的變數全部剔除，保留的都是顯著的。接著再對未引入回歸方程中的變數分別計算其偏回歸平方和，並選其中偏回歸方程和最大的一個變數，同樣在給定水平下作顯著性檢驗，如果顯著則將該變數引入回歸方程，這一過程一直持續下去，直到在回歸方程中的變數都不能剔除而又無新變數可以引入時為止，這時逐步回歸過程結束。
