簡介
逆變換採樣(英語:inverse transform sampling),又稱為 逆採樣(inversion sampling)、 逆機率積分變換(inverse probability integral transform)、 逆變換法(inverse transformation method)、 斯米爾諾夫變換(Smirnov transform)、 黃金法則(golden rule)等, 是偽隨機數採樣的一種基本方法。在已知任意機率分布的累積分布函式時,可用於從該分布中生成隨機樣本。
定義
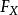 逆變換採樣
逆變換採樣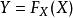 逆變換採樣
逆變換採樣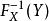 逆變換採樣
逆變換採樣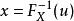 逆變換採樣
逆變換採樣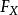 逆變換採樣
逆變換採樣假設X為一個連續隨機變數,其累積分布函式為。此時,隨機變數服從區間[0,1]上的均勻分布。逆變換採樣即是將該過程反過來進行:首先對於隨機變數 Y,我們從0至1中隨機均勻抽取一個數u。之後,由於隨機變數與X有著相同的分布,即可看作是從分布中生成的隨機樣本。
示例
假設有一個累積分布函式
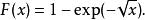 逆變換採樣
逆變換採樣我們要從該分布中生成隨機樣本。F(x)的反函式為:
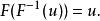 逆變換採樣
逆變換採樣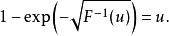 逆變換採樣
逆變換採樣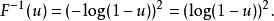 逆變換採樣
逆變換採樣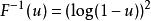 逆變換採樣
逆變換採樣於是,我們先從0至1中隨機均勻抽取 u,然後計算以得到我們需要的樣本。
