基本研究
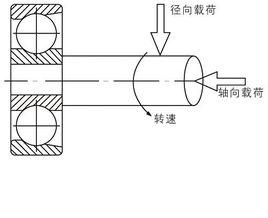
軸向載荷廣泛存在於各種結構振動中,它不僅在理論上有重要研究價值,而且有廣泛的工程背景。比如在火箭飛彈的飛行過程中,存在著很大的軸向壓縮載荷,這個軸壓載荷對飛彈橫向振動特性存在不同程度的影響。
目前軸向載荷對結構振動特性的影響已經得到國內外高度關注,主要體現在軸向載荷對薄壁梁彎扭耦合動力回響,以及穩定性分析;而英國J.R.Banerjee等人利用動態剛度矩陣法研究了軸向載荷對複合材料梁彎扭耦合振動特性的影響。
研究發現當彈性波在周期性複合材料或結構中傳播時,彈性波經過周期性調製,在特定的頻率範圍內不能傳播。人們將該頻率範圍稱為帶隙,而這種具有彈性波帶隙的周期性複合材料或結構則稱為聲子晶體。由於聲子晶體的帶隙特性可以有效控制彈性波的傳播,並且帶隙頻率範圍可人為設計,因而聲子晶體在聲學器件以及減振降噪方面具有廣泛的套用前景。
 軸向載荷
軸向載荷軸承種類中按照承受軸向載荷能力的從小到大依次是:圓柱滾子軸承<球軸承<圓錐滾子軸承<端面軸承。
軸向載荷的計算方法
公式法
第一種方法是直接寫出公式,此法在國內眾多文獻中可見到。
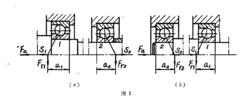
在一般計算中,如果Fa為軸線的方向,則軸承的軸向載荷可按下列兩式兩式算出,取其值較大者:
Fa1=S1
Fa1=S2+Fa
軸承的垂直軸線方向的軸向載荷可按下列兩式計算,取其數值較大者:
Fa2=S2
Fa2=S1一Fa
 軸向載荷
軸向載荷軸承上產生的對於與其配合軸承來說是一個外力,它和外加軸向載荷Fa同方向。文獻處理的方法的特點是比較簡單,但使用時必須注意向心推力軸承在軸上的安裝型式,型式不同時,軸承上的受力也不同。因此在計算軸向載荷時易發生錯誤。
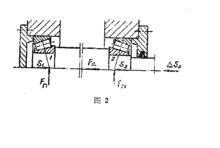
力平衡條件法
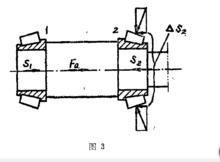
針對圖2的情況討論如下:若S1十Fa>S2時,由平衡條件可知:S1+Fa=S2+△S2。式中△S2為軸承端蓋對軸承2的附加反力。則作用在軸承2上的軸向載荷Fa2=S1+Fa,作用在軸承1上的軸向載荷Fa1=S1。
若S1+Fa<S2時,由平衡條件可知:
S2一Fa=S1+△S1
 軸向載荷
軸向載荷式中△S1為軸承端蓋對軸承1的附加反力。則作用軸承1上的軸向載荷Fa1=S2一Fa,作用在軸承2上的軸向載荷Fa2=S2。
分析法
軸承1上產生的派生軸向力S1對於軸承2來說是外力,使軸承2有壓緊的趨勢,故定S,為“十”。圖中外力口軸向力Fa也使軸承2有壓緊的趨勢,所以也定為“+”;故作用在軸承2上的軸向外力為(Fa+S1)。現就Fa+S1與S2的值相比較,討論如下:
(1)若Fa十S1=S2,即作用在軸承2上的軸向外力(Fa+S1)與軸向內力S2相等。顯然軸承2上的軸向載荷Fa2=S2=Fa+S1。
(2)若Fa十S1>S2,則軸承2有向右移動的趨勢,而軸承端蓋給軸承外圈反力△S2,△S2通過軸承外圈作用在軸承2中滾動體上的法向力如圖3所示,其中徑向分力相互平衡,而軸向分力使軸承2內向左方向的軸向內力增加△S2,從而使軸承2上所受的軸向外力與軸向內力相平衡,即:
Fa+S1=S2+△S2
所以作用在軸承2上的軸向載荷Fa2=Fa+S1。
(3)若Fa十S1<S2,則軸和軸承1有向左移動的趨勢,而左端的軸承蓋給軸承1反力△S1,從而使軸承2上所受的軸向外力與軸向內力相平衡,即:
Fa+S1+△S1=S2
故作用在軸承2上的軸向載荷為S2。
根據以上三種情況分析可知,作用在軸承2上的軸向載荷Fa2,只要看作用在軸承2上的外力(Fa+S1)或派生軸向力S2哪一個大,就取哪一個為Fa2。
 軸向載荷
軸向載荷實例分析
轎車輪轂軸承軸向載荷特性分析:針對轎車實際行駛工況,基於靜力學分析方法,建立簡化的轎車行駛單軌模型,對轎車輪轂軸承軸向載荷特性進行分析。
轎車輪轂軸承的外部載荷是複雜多變的。在實際行駛當中,路況、行車速度、轉彎半徑和輪胎特性等都顯著影響著輪轂軸承的壽命與性能。我們有汽車徑向、軸向的輪胎載荷計算公式,但沒有給出汽車在轉彎狀態下相應的計算方法或結果。從忽略曲線行駛阻力、輪胎切向力以及滾動阻力等,建立線性化的汽車剛體開始。
輪轂軸承的外部載荷通過輪胎施加在輪轂軸承上,即在轎車的實際行駛過程中,路面對輪胎的徑向、軸向載荷等間接作用在了輪轂軸承上。根據力的傳遞特性,可認為輪轂軸承外部載荷等價於輪胎的外部載荷。汽車的側向加速度由汽車轉彎半徑和行駛速度直接決定,其中,汽車的轉彎半徑與前輪轉向角緊密聯繫。
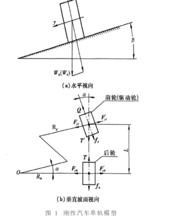
分析表明:由於車身結構的固有頻率大多低於15Hz,所以當轎車在行駛時的振動頻率低於15Hz時,可將車身運動假設為剛體運動。並且,轎車前、後部分質量耦合關係不明顯。忽略汽車轉向系、輪胎和懸架的慣性、阻尼、彈性等非線性特性因素以及汽車橫擺,假設汽車質心在路面上,並且系統是線性的,質心上作用的離心力不會改變兩側載荷的大小,即認為汽車只有前、後兩個輪胎,質心在連線前、後輪的剛性架上,將轎車運動簡化成為基本的線性化剛體運動,建立起剛性的汽車線性單軌模型。
 軸向載荷
軸向載荷汽車的坐標系固定於輪胎中心,其原點與輪胎的幾何中心重合。設定x軸指向輪胎正前方,y軸指向左側,z軸通過輪胎質心指向正上方。考慮一般情況,以前輪驅動的轎車為代表,汽車在橫坡角為β的坡道上以固定轉向角α和恆定速度v穩態轉彎,建立剛性汽車單軌模型如下圖所示。
軸向載荷對載荷分布的影響
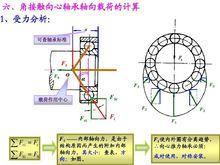
當向心推力軸承承受徑向載荷R時,由於滾動體與滾道的接觸線與軸承軸線之間夾一個接觸角α,因而各滾動體的反力Ni並不指向半徑方向,而是沿接觸點的法線方向,它可以分解為一個徑向分力和一個軸向分力。用Pi代表某一滾動體反力的徑向分力,則相應的軸向分力Fdi應等於Pi tanα。所有徑向分力Pi的合力R’與徑向載荷R相平衡;所有的軸向分力Fdi之和組成軸承的派生軸向力Fd,它迫使軸頸(連同軸承內圈和滾動體)向右移動,並最後與軸向力Fa平衡。
當只有一個滾動體受載時,即載荷角和接觸角相等。當受載的滾動體數目增多,雖然在同樣的徑向載荷Fr的作用下,但派生的軸向力Fd將增大。因這時作用於各滾動體上的徑向反力Pi的方向各不相同,它們的向量和R’雖然與Fr平衡,但其代數和必大於Fr,而派生的軸向力Fd是由各個Pi分別派生的軸向力Fdi合成的,其值應按Fdi的代數和計得。所以在同樣的徑向載荷Fr作用下,由作用於各滾動體上Pi的分別派生的軸向力所合成的軸向力Fd,將比只有一個滾動體受載時派生的軸向力大。
以上分析說明:
(1)向心推力軸承必須在徑向載荷R和軸向力A的聯合作用下工作。
(2)對於同一軸承,在同樣的徑向載荷R作用下,當受載的滾動體數目不同時,就派生出不同的軸向力S,也就需要不同的軸向力A來平衡它。或者反過來說,在徑向載荷R不變的條件下,當軸向力由最小值(Fa=Fr*tanα)這時由一個滾動體受載)逐步增大(即β角增大),這意味著軸承內接觸的滾動體數目逐漸增多。
對實際工作的向心推力軸承,為保證它能可靠地工作,應使它至少達到下半圈滾動體全部受載。因此安裝這類軸承時,不能有較大的軸向竄動。