簡介
金融數學中、 赫爾懷特模型(英:Hull-White model)、是利率模型的一種。此模型中、為了把未來利率的變動變換成數學上較簡潔的Lattice model,將利率當作百慕達選擇權(選擇權存續期間中設定複數個期間,在這些期間可以執行的選擇權),以此便能將利率的變動價值以選擇權模評價型來評價。
赫爾懷特模型的原型是由約翰·赫爾和艾倫·懷特在1990年發表的,此模型今日仍經常實際在市場上使用。
模型構成
單一要素模型
此模型假設短期利率服從下面的隨機微分方程式:
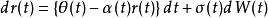 赫爾懷特模型
赫爾懷特模型然而不論哪個變數都可以假定跟時間相關,因此依對各變數的假設,一般實務上作以下的區別:
•θ是常數 ─瓦西塞克模型
•θ是跟時間相關的變數 ─ 即赫爾·懷特模型
•θ還有α都是跟時間相關的變數 ─ 赫爾·特模型對瓦西塞克模型,又稱為擴展瓦西塞克模型。
雙要素模型
雙要素赫爾懷特模型 (Hull 2006,pp.657–658) 假設利率的變動服從以下的隨機過程:
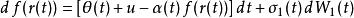 赫爾懷特模型
赫爾懷特模型 赫爾懷特模型
赫爾懷特模型方程中的的初始值為零並且服從下面的隨機過程:
 赫爾懷特模型
赫爾懷特模型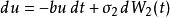 赫爾懷特模型
赫爾懷特模型也就是雙要素赫爾懷特模型,多了一個記為的隨機過程,作為干擾項。
 赫爾懷特模型
赫爾懷特模型以下說明基本的 赫爾懷特模型、也就是只有 θ,沒有額外的干擾項。 若目前的利率水準相當高(即 r> θ( t)/ α), 利率在服從此一隨機微分方程下,對時間的漂移項變動量將會是負值;若目前的利率水準相當低,則漂移項的變動量將會為正。也就是說利率的隨機過程將會服從平均奧恩斯坦-烏倫貝克過程。)
θ是由利率期間結構曲線計算而來,而α代表的是利率的變動朝著θ收斂回歸的速度,是由使用者自行設定的係數,一般由歷史資料推估而來。σ是由市場上所存在可以交易的利率交換選擇權跟利率上限選擇權的波動校正項歷史資料所計算得知。
當 α、 θ、 σ為常數,依伊藤引理可以證明以下方程成立。
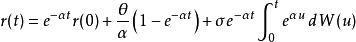 赫爾懷特模型
赫爾懷特模型且服從常態分配:
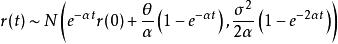 赫爾懷特模型
赫爾懷特模型樹狀圖
然而利率上限選擇權與利率交換選擇權等較為單純的金融商品,通常作為波動校正係數的測量。此模型真正的用處,是用來評價在樹狀圖上表示方式相當複雜,如百慕達選擇權這類的新奇選擇權的評價。
關聯項目
•金融工程學
•金融數學
•瓦西塞克模型
•Cox–Ingersoll–Ross model
