簡介
費雪變換(英語:Fisher transformation)是統計學中用於相關係數假設檢驗的一種方法。對樣本相關係數進行費雪變換後,可以用來檢驗關於總體相關係數ρ的假設。
定義
已知 N組雙變數樣本( X, Y), i=1,..., N,樣本相關係數 r為
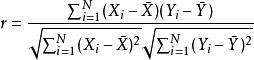 費雪變換
費雪變換於是, r的費雪變換可定義為
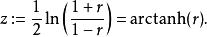 費雪變換
費雪變換當 (X,Y) 為二元常態分配且 (X,Y)對相互獨立時,z近似為常態分配。其均值為
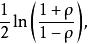 費雪變換
費雪變換標準差為
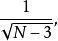 費雪變換
費雪變換其中 N是樣本大小,ρ 是變數 X與 Y的總體相關係數。
費雪變換及其逆變換
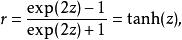 費雪變換
費雪變換可以用於構造ρ的置信區間。
討論
當X和Y遵循二元常態分配時,Fisher變換是r的近似方差穩定變換。這意味著對於群體相關係數ρ的所有值,z的方差近似恆定。在沒有Fisher變換的情況下,r的方差隨著|ρ|變小由於Fisher變換大約是| r |時的恆等函式<1/2,有時候有必要記住r的方差很好地接近1 / N,只要|ρ|不是太大,N也不是太小。這與二元正態數據的r的漸近方差為1的事實有關。
自從費希爾於1915年引入這種變換以來,這種變換的行為已經得到了廣泛的研究。費舍爾自己在1921年發現了二元常態分配數據的z的精確分布; 1951年Gayen確定了來自雙變數A型Edgeworth分布的數據的z的精確分布。 1953年霍特林計算了z的矩和泰勒級數表達式以及幾個相關的統計量,而霍金斯在1989年發現了具有有界四階矩的分布數據的z的漸近分布。
套用
雖然Fisher變換主要與雙變數正態觀測的Pearson積矩相關係數有關,但在更一般的情況下,它也可以套用於Spearman秩相關係數。類似結果對於漸近分布適用,但需要較小的調整因子。
各種相關係數
對於不同測量尺度的變數,有不同的相關係數可用:
•Pearson相關係數(Pearson'sr):衡量兩個等距尺度或等比尺度變數之相關性。是最常見的,也是學習統計學時第一個接觸的相關係數。
•淨相關(英語:partial correlation):在模型中有多個自變數(或解釋變數)時,去除掉其他自變數的影響,只衡量特定一個自變數與因變數之間的相關性。自變數和因變數皆為連續變數。
•相關比(英語:correlation ratio):衡量兩個連續變數之相關性。
•Gamma相關係數:衡量兩個次序尺度變數之相關性。
•Spearman等級相關係數:衡量兩個次序尺度變數之相關性。
•Kendall等級相關係數(英語:Kendall tau rank correlation coefficient):衡量兩個人為次序尺度變數(原始資料為等距尺度)之相關性。
•Kendall和諧係數:衡量兩個次序尺度變數之相關性。
•Phi相關係數(英語:Phi coefficient):衡量兩個真正名目尺度的二分變數之相關性。
•列聯相關係數(英語:contingency coefficient):衡量兩個真正名目尺度變數之相關性。
•四分相關(英語:tetrachoric correlation):衡量兩個人為名目尺度(原始資料為等距尺度)的二分變數之相關性。
•Kappa一致性係數(英語:K coefficient of agreement):衡量兩個名目尺度變數之相關性。
•點二系列相關係數(英語:point-biserial correlation):X變數是真正名目尺度二分變數。Y變數是連續變數。
•二系列相關係數(英語:biserial correlation):X變數是人為名目尺度二分變數。Y變數是連續變數。
參見
•數據轉換(統計)
•Meta分析(此變換用於meta分析以穩定方差)
•部分相關性
