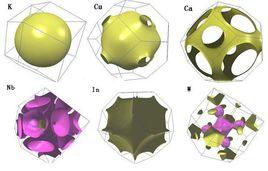
定義
費米面是最高占據能級的等能面,是當T=0時電子占據態與非占據態的分界面。一般來說,半導體和絕緣體不用費米面。而用價帶頂概念。金屬中的自由電子滿足泡利不相容原理,其在單粒子能級上分布幾率遵循費米統計分布。
費米面的構造
費米能級是電子占有態和未占有態的邊界面,在三維空間中費米能級就是k空間中能量為EF的曲面,即E= EF(k)=C所構成的曲面為費米面。k空間中被充滿區域的總面積僅僅依賴於電子濃度,而費米面的形狀依賴於點陣的相互作用.費米面附近的電子對金屬的性質有重要影響,如金屬的電子比熱、電子的脫出功、金屬電導等主要決定於費米面附近的電子,有人甚至把金屬定義為具有費米面的固體。顯然了解和掌握費米面的概念以及距布氏區邊界多遠的問題是對金屬中電子的物理特性獲得深刻理解的根本問題.
二維金屬費米面的描繪
在當前的固體物理學教材中,對費米面的構造沒有詳細的闡述。費米面附近的電子對金屬的性質有重要的影響,了解和掌握費米面的構造以及其在布里淵區中的填充情況是對金屬中電子的物理特性獲得深刻理解的一個根本問題。
絕對零度下,電子在波矢空間(k空間)中分布(填充)而形成的體積的表面稱為費米面。由於在絕對零度時電子都按照泡利不相容原理填滿於費米面以下的量子化狀態中,所以費米面也就是k空間中費米能量所構成的表面,且費米面是一等能面。實際晶體的能帶結構十分複雜,相應的費米面形狀也很複雜,最簡單的情況是理想電子氣的費米面,它是一個以k為半徑的費米球。
費米能級是電子占有態和未占有態的界面,在三維空間中費米能級就是k空間中能量為EF的曲面,即E=EF(k)=C所構成的曲面為費米面。費米面附近的電子對金屬的性質有重要影響,如金屬的電子比熱、電子的脫出功、金屬電導等主要決定於費米面附近的電子,有人甚至把有金屬定義為有費米面的固體。
布里淵區角頂附近的費米面
在導體中靠近布里淵區角頂的費米面具有特殊的凝聚和破缺效應。這種效應有可能導致電子氣的相變。因此,有必要對此角頂附近的電子分布作更深入的數值計算,研究費米面的特徵。在計算中同時考慮晶格的周期場和電子(自旋平行)的交換能。為了具體化,我們以鋁金屬為實例進行計算。
計算方法是從角頂開始,將電子放入角內一層一層的等能量費米面,各方向射線上的k波矢量值不相同。用變分法求出角頂近旁單電子Bloch波及其能級。然而加入電子間的交換能計算費米面上電子的能量;由上一層的費米面確定出下一層加上去的費米面。晶格周期場採取Heine所給值。
計算結果給出不同波矢量組的費米面;費米面上電子能量,費米面電子數。費米面不呈球形而是有幾個極大和極小的扭曲面,中間突出,在邊界上低平。當波矢量增大時,扭曲程度縮小。電子能量先變小然後到極小值,之後便急速上升。在極小時,電子密度達到10 個/cm 的量級,相當於有相關長度10 cm.
為了能粗估分布角區中電子有對角分布對稱時破缺的可能性,在附錄中估計了在同一角區中和不同角區中兩個電子的交換能。初步計算結果,在極小值附近,兩電子在不同角區中交換能比在同一個角區中交換能要小3倍。這就說明有破缺的可能性。這個破缺和Bloch有關最低能級中無穩電流的分析論證,將在另一文中發表。這破缺的來源是由於:當波矢量增大時,簡供的波函式急速轉變成非簡拼的前進波,這使交換能突然變少,而交換能的凝聚作用引起費米面按角頂不同而各自分裂。這種分裂必然引起相變。而極小值的出現就是破缺的開始。
UGe2在鐵磁態下費米面
1.UGe2的晶格結構及色散關係
 費米面
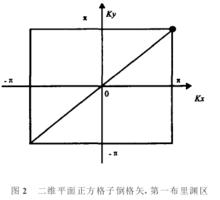
費米面Shick和Pickett研究認為,UGe2的結構是準二維結構,在這裡我們把它看作二維正方格子,則它的倒空間也是正方格子,它的第一布里淵區也是平面正方形,如圖2所示.
2.費米面
若我們取格點上電子半滿,即取μ=0,取σh = 0.5t,溫度為絕對零溫。則令ε=0,根據式子得到有磁場時的費米面.因為二維正方格子第一布里淵區(如圖2所示)為正方形,關於k、k和原點對稱,所以只需畫出第一象限的費米面,如圖3所示。
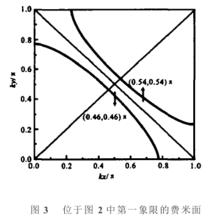 費米面
費米面圖3中,二維動量空間範圍是k∈(0,π);ky∈(0,π)。圖中由坐標(0, 1)到坐標(0, 1)的斜細直線為UGe2處於非鐵磁態時電子的費米面,而直的斜線左下面的粗的曲線表示的是自旋向下電子的費米面,直斜線右上方的粗曲線表示自旋向上電子的費米面。