定義
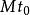 負維空間
負維空間 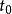 負維空間
負維空間 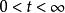 負維空間
負維空間 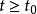 負維空間
負維空間 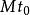 負維空間
負維空間 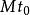 負維空間
負維空間 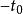 負維空間
負維空間 假設是郝斯多夫維數的緊空間且是互相嵌入的緊空間元素並令參數t為零到無限()。若緊空間中構成這些元素都是時,這個尺度就能視為與等價。這時就可以說緊空間是這個尺度等價集合的洞,而是對應的等價類的負數維度。
歷史
1940年代時,拓撲結構科學已有相當程度的發展,對於正維度拓樸空間基本理論的研究也十分完備。在數值計算和一定程度美學的動機下,拓樸學家開始尋找能擴展空間概念、允許負數維度的數學框架。但這樣的維度就像四維和更高的維度難以想像也無法直接觀察。直到1960年代時才建構了一個特殊的拓樸框架,即拓樸譜學的範疇。拓樸譜學是允許負維空間的一般化。負維空間的概念已經有實際用途了,如分析語言統計學。
拓撲空間
 負維空間
負維空間  負維空間
負維空間 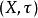 負維空間
負維空間  負維空間
負維空間  負維空間
負維空間 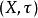 負維空間
負維空間  負維空間
負維空間 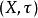 負維空間
負維空間 拓撲空間是一個集合 和其上定義的拓撲結構組成的二元組。 的元素 通常稱為拓撲空間 的點。而拓撲結構一詞涵蓋了開集,閉集,鄰域,開核,閉包,導集,濾子等若干概念。從這些概念出發,可以給拓撲空間作出若干種等價的定義。在教科書中最常見的定義是從開集開始的。
負一維空間
在抽象幾何學中,負一維空間表示比零維空間還低一個維度的負維空間,其代表了空多胞形本身的維度,由於空多胞形是一個空集合,因此負一維空間也等於一個 空空間(英語:null space、或稱虛無空間、零空間)。也可以定義更低的維度作為空多胞形的基底,即 超空多胞形(英語:Dinull polytope)。
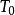 負維空間
負維空間 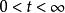 負維空間
負維空間 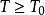 負維空間
負維空間  負維空間
負維空間 負一維是一切多胞形的最終基礎。假設0是一個緊湊的Hausdorff維數空間,這是一個規模緊緻空間的相互嵌入和參數化的T的一個元素()。這樣的尺度要考慮0如果構成的緊湊空間一致的等效。據說,緊湊的空間0是在等效天平的孔,和是相應的等價類的負維度。
參見
• 數學主題
• 負一維空間
