貝努利模型概述
n重貝努利實驗：重複進行n次獨立的貝努利試驗，這裡“重複”的意思是指各次試驗的條件是相同的，它意味著各次試驗中事件發生的機率保持不變。“獨立是指是指各次試驗的結果是相互獨立的。基於n重貝努利試驗建立的模型，即為貝努利模型。
模型套用於相互獨立的事件上，如投硬幣，新生兒性別等。
貝努利模型的過程
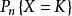貝努利模型設實驗結果只有兩個即A或Ã，且P（A）=p，P（Ã）=1-p=q，獨立的重複的進行n次實驗，在n重貝努利模型事件A恰恰出現K次的機率常稱為二項機率，通常與實際情況相符，這個機率常稱為二項機率。記為
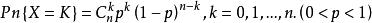貝努利模型則有
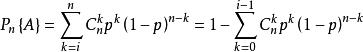貝努利模型（A至少發生i次）
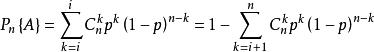貝努利模型（A至多發生i次）
在n重貝努利試驗中，事件A發生的次數ξ是一個隨機變數，它可以取0、1、2……n共n+1個可能值。關於貝努利試驗，有如下的重要定理。
對於貝努利概型，事件A在n次試驗中發生k次的機率為 Pn（k）=Cnkpkqn-k （0≤k≤n） (公式1)
事件A至多出現m次的機率是 m P{0≤ξ≤m} = ∑Cnkpkqn-k (公式2)
K=0 事件A出現次數不小於l不大於m的機率是 m P{l≤ξ≤m}= ∑ Cnkpkqn-k (公式3)
K=l 貝努利分布的期望 E(ξ)=np (公式4)
給定出現A的幾率為p，用上面的公式就可以計算出試驗次數為n時的幾率。
當n為偶數時，計算公式為 n P{n/2+1≤ξ≤n}= ∑ Cnkpkqn-k (公式5)
K=n/2 當n為奇數時，計算公式為 n P{n/2+1≤ξ≤n}= ∑ Cnkpkqn-k (公式6)
K=n/2+1 其中K=n/2+1取整數。
