簡介
晶體在外界條件(變形、冷凝、電解及熱處理等)作用下,沿某些晶體位向的擇優取向稱作織構。按形成方式,主要有:通過液態金屬冷凝形成的稱“鑄造織構”;通過塑性變形形成的稱“形變織構”;在塑性變形後經退火形成的稱“退火織構”。具有織構的金屬材料呈現明顯的各向異性。同一材料根據加工方式的不同可出現不同的形變織構,按照坯料或製品的外形,形變織構可分為絲織構和板織構。在拉伸(拉絲)、擠壓和旋鍛條件下形成的織構稱為絲織構,這時晶體中晶粒有一個共同的晶向相互平行,並和棒材(線材)軸向一致。
板織構又稱軋制織構。在軋制條件下形成的織構稱為板織構。板織構不僅晶粒的晶向平行軋制時最大主變形方向(SLN方向),而且某一結晶學平面平行於板材表面。
具有冷變形織構的材料進行退火時,由於晶粒位向趨於一致,總有某些位向的晶塊易於形核及長大,故形成具有織構的退火組織,稱為退火織構又叫再結晶織構。具有退火織構組織的材料的金相組織觀察為等軸的晶粒,但他們的取向又是一致的。
分類
類別 按變形方式不同,變形織構可分為拉絲織構、擠壓織構、鍛造織構和軋制織構等;按織構類型可分為絲織構(線織構)、面織構和板織構等。
多晶體金屬在單向塑性變形(如拉拔,沿一個方向軋制)時,各晶粒在滑移的同時,其滑移系還發生朝外力方向的轉動,當變形量很大時,經轉動後的各個晶粒最終會趨於同一位向,於是產生了織構。這種由變形過程中產生的織構稱為“變形織構”。
依加工方式的不同,變形織構可分為兩類:
(1)絲織構,在拉拔時形成,其特徵是各個晶粒的某一晶向與拉拔方向平行或接近於平行,如下圖(a)所示。絲織構以與線軸平行的晶向<刪>來表示,如冷拉鐵絲為[110]織構,冷拉銅絲為[111]+[100]織構。
 變形織構
變形織構(2)板織構,在軋制時形成,其特徵是各晶粒的某一晶向平行於軋制方向,某一晶面趨向於與軋制面平行,如下圖(b)所示。板織構以與軋制面平行的晶面(hkl)和與軋制方向平行的晶向[uvw]來表示,記為(hkl)[uvw]。例如面心立方金屬的板織構有兩種,一種是(110)[112],稱為黃銅型織構,另一種是(112)[111],稱為銅型織構。
應當指出,織構不是對晶粒形狀的描述,而是表示多晶體金屬中各晶粒取向大致趨於一致的晶體結構特徵。完全理想的織構,其取向應當如同單晶。但實際多晶體金屬的織構中,晶粒取向的集中程度往往不很高。
形成變形織構
金屬中晶粒的位向一般是無規則排列的,所以巨觀性能表現為各向同性。當金屬發生塑性變形時,各晶粒的晶格位向會沿著變形方向發生轉變。當變形量很大時(>70%),各晶粒的位向將與外力方向趨於一致,晶粒趨向於整齊排列,稱這種現象為擇優取向,所形成的有序化結構稱為變形織構。
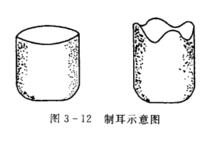 制耳示意圖
制耳示意圖變形織構的產生,在許多情況下是不利的。變形織構會使金屬性能呈現明顯的各向異性。各向異性在多數情況下對金屬後續加工或使用有不利的影響。例如,用有織構的板材沖制筒形零件時,由於不同方向上的塑性差別很大,使變形不均勻,導致零件邊緣不齊,即出現所謂“制耳”現象,如圖所示。但變形織構在某些情況下是有利的,例如製造變壓器鐵芯的矽鋼片,利用變形織構可使變壓器鐵芯的磁導率明顯增加,磁滯損耗降低,從而提高變壓器的效率。
變形織構很難消除。生產中為避免織構產生,常將零件的較大變形量分為幾次變形來完成,並進行“中間退火”。
變形織構模型
許多科學工作者致力於變形織構形成理論的研究,提出了許多塑性變形模型,主要有薩克斯(E.Sachs)模型和泰勒(G.I.Taylor)模型,其他模型基本上是由它們派生出來的。1928年薩克斯假定各晶粒的受力狀態都等於樣品的巨觀受力狀態,並假定各滑移繫上臨界分切應力τ為常數,當滑移繫上的分切應力達到τ時,該滑移系啟動。若已知外施應力狀態σ則滑移系s上的分切應力τ=mσ(i,j=1,2,3)。式中ij重複表示求和,m=(n a b) a,n為滑移系。滑移平面的法向矢量; b為滑移方向矢量; a為應力張量σ坐標系矢量;括弧內字母重複表示不求和。該模型適用於單晶體的自由變形,按最大取向因子m選取滑移系s。但該模型對多晶體來說,忽視了各晶粒之間變形的相互限制和協調,各晶粒之間會形成“孔洞”或‘‘堆集”。一些研究者放鬆了晶體的變形只由最大取向因子選取滑移系的限制,或者規定了對變形體外形的限制。儘管這樣,該模型難以描述多晶體的塑性變形。1938年泰勒提出另一塑性變形模型,假定金屬中各晶粒的變形狀態與樣品的巨觀變形狀態相同。根據該模型,又考慮體積守恆及dε=1/2(m+mdγ(見微觀塑性力學)關係,要進行晶體的塑性變形至少需要啟動5個滑移系。fcc金屬通常有12個滑移系,因此滑移系的選取有C=792種可能,但獨立的滑移系只有384種。為了確定所需滑移系,泰勒選取的原則是使晶體塑性變形的總剪下量dτ=∑dγ最小。20世紀50年代畢肖普(J.F.W.Bishop)和希爾(R.Hill)用最大外功原理求解滑移系:對於一個給定的應變狀態,所選擇的滑移系應滿足外力所做的功δW=σδε為最大。1969年陳煜耀(G·Y·Chin)等證明了以上·t兩個原則’’是等價的。但科克斯(U.F.Kocks)用該原理對fcc金屬只能求出6或者8個滑移系,因此5個滑移系的求算具有不確定性。要解決不確定性問題,需要引入附加的原則或方法。平均轉動法用晶體的平均轉動計算每一晶粒方向的變化;鬆弛限制法將所施加的應變(或應變速率)分量減少1個或者2個;塑性功二次最小二乘法通常可使滑移量和晶格轉動惟一確定;速率敏感模型使屈服角變圓,使與給定頂點相關的不同滑移系的分切應力值不同。
泰勒模型忽視了晶體的彈性應變、各晶體的非均勻應變、晶界處應力的平衡以及晶體的加工硬化。儘管如此,與薩克斯模型相比,實驗表明它比較適用於多晶材料的變形,因此,許多變形模型都是基於泰勒模型進行修正發展的。修正的泰勒模型放鬆了巨觀應變的嚴格限制,考慮了晶界處的變形和應力的可傳遞性以及晶粒的大小與形狀等情況。基於各修正的模型所預測的晶體取向分布更接近實際的結果。
基於上述原則,當滑移系(n,b)確定以後,各滑移系的剪下量dγ隨即確定。考慮晶體中某矢量A,當滑移系(n,b)啟動並產生了dγ的剪下變形時,則A變到A’=A+dγ(An)b;若有K個滑移系啟動,則
A’=A+∑(dγ(An)b)
由該式可計算晶體產生滑移塑性變形後取向的變化。
