基本介紹
對參考點的衝量矩
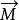 衝量矩
衝量矩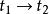 衝量矩
衝量矩衝量矩是過程量,是時間的函式,定義對參考點的衝量矩為力對參考點的力矩 對時間的累積,即在 時間內,力矩對參考點的衝量矩為
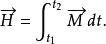 衝量矩
衝量矩對時間的平均力矩
對時間的平均力矩定義為:
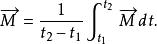 衝量矩
衝量矩對參考軸的衝量矩
對參考軸的衝量矩:
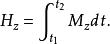 衝量矩
衝量矩定理
衝量矩定理(theorem of moment of impulse)是動量矩定理的積分形式。質點系對固定點O (或定軸x)的動量矩在時間間隔t-t中的改變, 等於作用在該系統上的諸外力在這段時間內對該點 (或該軸)的衝量矩的矢量和(或代數和)。即
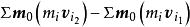 衝量矩
衝量矩或
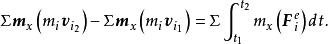 衝量矩
衝量矩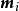 衝量矩
衝量矩 衝量矩
衝量矩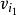 衝量矩
衝量矩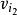 衝量矩
衝量矩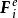 衝量矩
衝量矩式中 是任意質點 的質量; 與 分別為該質 點在瞬時t與t的速度; 為作用於該質點的系統的外力。
力矩
力對參考點O點的力矩
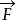 衝量矩
衝量矩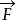 衝量矩
衝量矩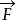 衝量矩
衝量矩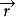 衝量矩
衝量矩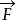 衝量矩
衝量矩一個常力作用在一個一端點固定且可以繞此固定點轉動的細桿上,力的作用點距固定點的距離和力的方向不同,其作用效果是不同的,所以僅僅用力 不能完全描述桿的轉動狀態的改變,為了描述它的轉動狀態改變,我們必須引入一個不僅與力 有關,而且還與力的作用點相對於參考點(如桿端的固定點作參考點)的位矢有關的物理量,即 力矩的概念,設力 的作用點對參考點 O的位矢為 ,則力 對參考點O的力矩定義為
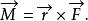 衝量矩
衝量矩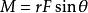 衝量矩
衝量矩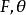 衝量矩
衝量矩 衝量矩
衝量矩它的大小為: ,顯然當 不變,r越大,力矩大小M也越大,桿的轉動角速度變化就越大;反之,亦然,當 =0,即力沿著桿的方向作用,力矩等於零,桿的轉動狀態也不變,所以力矩是改變物體轉動狀態的原因.
說明:
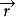 衝量矩
衝量矩 衝量矩
衝量矩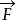 衝量矩
衝量矩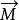 衝量矩
衝量矩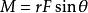 衝量矩
衝量矩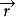 衝量矩
衝量矩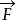 衝量矩
衝量矩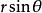 衝量矩
衝量矩(1)由矢積的性質可知,力矩是矢量,它的方向由右手螺旋法則確定:即右手伸直,拇指垂直於四指,四指指向位矢 的方向沿小於 的角度轉向力 的方向時,拇指所指的方向就是力矩 的方向,它的大小為 ,即等於由 和 構成平行四邊形的面積,其中 是參考點到力的作用線的距離,稱為力對參考點O的 力臂。
(2)對於質點系,內力是以作用力和反作用力形式成對出現,任意一對內力均是牛頓力,它們對任意參考點的力矩均為零,所以,質點系所有內力對任意參考點的力矩矢量和為零。
(3)力矩的大小和方向都與參考點O的選擇有關。因此,在計算力矩時,必須說明參考點。
(4)力矩單位為牛 米(N m),但不能寫成焦耳 。
(3)力矩在空間直角坐標系中的分量式為
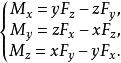 衝量矩
衝量矩力對固定轉軸的力矩
設固定轉軸為z,則力對於固定轉軸的力矩就是其對z軸的力矩,即
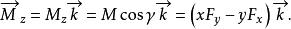 衝量矩
衝量矩