定義
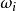藏本模型
藏本模型在藏本模型最常見的版本中，每個振子都有一個固有的自然頻率 ，並與所有其它振子以相同的強度耦合。驚人的是，在 的極限下，通過巧妙的變換並使用平均場方法，這個完全非線性的模型是可以精確求解的。
這個模型最常見的形式由以下方程組給出：
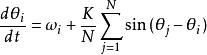藏本模型
藏本模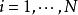型
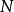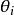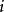藏本模型
藏本模型
藏本模型
藏本模型。系統由 個極限環振子組成， 是第 個振子的相位， 是耦合強度。
也可以在系統中加入噪聲。這種情況下，方程變為
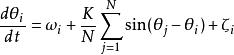藏本模型
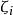藏本模型其中 是漲落，並且是時間的函式。
變換
定義序參量
藏本模型
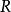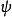藏本模型
藏本模型表征了這群振子的相位相關性， 是平均相位。方程可以改寫為
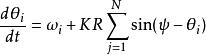藏本模型這樣振子的方程組就不是顯式耦合的，相反，序參量支配了系統的行為。
大N極限
藏本模型
藏本模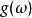型
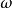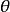藏本模型
藏本模型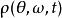
藏本模型
藏本模型考慮 的情況。自然頻率的分布記為 ，設在時刻 ，在所有自然頻率為 的振子中，相位為 的振子所占比例為 。歸一化要求
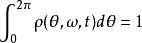藏本模型振子密度的連續性方程為
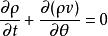藏本模型
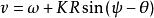藏本模型其中 是振子的游移速度。在連續極限下重新寫出序參量
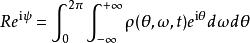藏本模型解
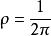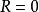藏本模型
藏本模型所有振子隨機漂移的不相關態對應均勻分布解 。這種情況 ，振子之間沒有關聯。系統整體處於統計穩定的狀態，儘管每個振子單獨來看都在以自然頻率不停運動。
當耦合足夠強時，可能會出現完全同步的解。在完全同步態中，所有振子以相同頻率運動，但相位可以不同。
部分同步是只有一些振子同步，而另一些振子自由漂移的狀態。對鎖相的振子
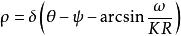藏本模型對漂移的振子
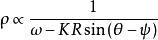藏本模型與哈密頓系統的聯繫
耗散的藏本模型包含在某些保守的哈密頓系統中，哈密頓量具有形式：
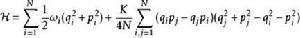藏本模型
藏本模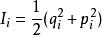型
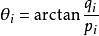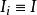藏本模型
藏本模型用正則變換變成作用量-角度的形式，作用量為 ，角度（相位） ，在作用量 為常數的不變流形上就是藏本動力學。變換後的哈密頓量
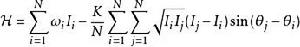藏本模型哈密頓運動方程為
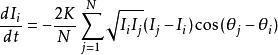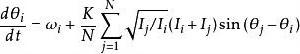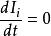藏本模型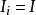
藏本模型
藏本模型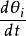
藏本模型
藏本模型因為 ，所以 確定的流形是不變的。並且相位動力學 就是藏本模型的動力學。
模型的變體
模型有兩種類型的變體，一種改變模型的拓撲結構，另一種改變耦合函式的形式。
改變拓撲
除了具有全連拓撲的原始模型，足夠稠密的複雜網路拓撲也可以用同樣的平均場處理。而對於局域的行為，例如鏈形或環形網路上的情況，不能再使用經典的平均場方法，所以只能具體問題具體分析，儘可能利用對稱性獲取解的信息。
改變相位的相互作用
藏本把兩個振子之間的相位相互作用用第1個傅立葉分量來近似。通過把高階傅立葉分量包括進來，可以得到更好的近似。高階項的引入也能帶來有趣的同步現象，例如異宿環、部分同步態、以及奇美拉態。
