基本介紹
二階和三階行列式按下圖所示進行計算:實線上的元素的乘積帶有正號,虛線上的元素的乘積帶有負號,並將這些乘積相加,得到二階與三階行列式的展開式。
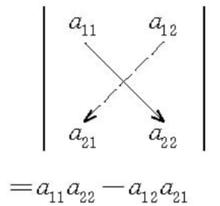 圖1 二階行列式按薩魯斯法則展開
圖1 二階行列式按薩魯斯法則展開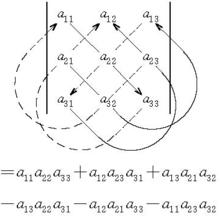 圖2 三階行列式按薩魯斯法則展開
圖2 三階行列式按薩魯斯法則展開這種計算方法稱為薩魯斯法則。在n階行列式D=|a|中,從左上角到右下角稱為D的主對角線,元素a,a,…,a稱為主對角線上的元素,簡稱主對角元;從右上角到左下角稱為D的次對角線,而元素a,a,…,a稱為次對角線上的元素,簡稱次對角元,因而,薩魯斯法則亦稱對角線法則 。
只有二階和三階行列式具有薩魯斯法則,四階及以上的行列式不存在薩魯斯法則 。
例題解析
【例1】計算三階行列式
 薩魯斯法則
薩魯斯法則解:由三階行列式的薩魯斯法則,有
 薩魯斯法則
薩魯斯法則【例2】設a+b+c= 0,求
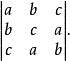 薩魯斯法則
薩魯斯法則提示:按薩魯斯法則展開,再分解因式。
解答案為0。
因為a+b+c=0,所以c=-a-b,按薩魯斯法則有
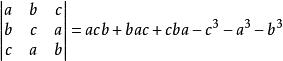 薩魯斯法則
薩魯斯法則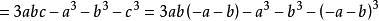 薩魯斯法則
薩魯斯法則 薩魯斯法則
薩魯斯法則【例3】求行列式
 薩魯斯法則
薩魯斯法則的展開式中x的係數。
提示:不必全部展開,從薩魯斯法則分析含x的項即可。
解答案為2。
根據薩魯斯法則,行列式中含有x的項有兩項:1·x·1項取正號,(-1)·x·1項取負號,兩項合併後內2x,故x的係數是2 。

