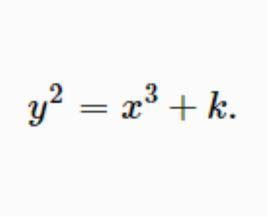基本介紹
莫德爾方程是一種著名的二元三次不定方程，指k為整數的不定方程
莫德爾方程多數莫德爾方程具有整數解，雖然只有有限個，但能求出它的全部解也是很困難的事，即使k很小。對某個k，求出它的全部解，有時是一篇論文的主題。
例如，1954年的一篇博士論文就是求莫德爾方程y²=x³+17(y>0)的全部整數解(x，y) = (﹣1，4)，(﹣2，3)，(2，5)，(4，9)，(8，23)，(43，282)，(52，375)，(5234，378661)，共八組解 。
關於莫德爾方程的一些結果
費馬(Fermat，P.de)在評註丟番圖(Diophantus，(A.))《算術》的頁邊注中宣布：他發現了一個美妙而精巧的方法，證明了方程y²=x³-2僅有一組正整數解(x，y)=(3，5)，但他的證明未找到，引起了許多數學工作者去探索方程(1)的解法。從歐拉(L.Euler)到近代的哈爾(A.Haar)、莫德爾(L.J.Mordell)、貝克(A.Baker)都曾研究過它。人們的探索豐富和發展了數論的內容，並得到一些有普遍意義的方法。如初等數論方法、代數數論方法。他們利用同餘式和二次剩餘理論對不定方程(1)首先得到下面結果：
1.當a，b為整數，且a沒有4t+3形狀的素因子時，不定方程y²=x³+(4b-1)³-4a²沒有整數解，由此可知，方程y²=x³-5，y²=x³-17，y²=x³+11均無整數解。
2.當a，b為整數，且2a+1沒有4t+3形狀的素因子時，不定方程y²=x³+(4b+2)³-(2a+1)²無整數解。
3.當a≡2，4(mod 8)，b≡1(mod 2)，且b沒有8t±3形狀的素因子時，方程y²=x³+2b²-a³無整數解 。
莫德爾方程4.當a≡4(mod 8)，b≡1(mod 2)，且b無形如8t+5和8t+7的素因子時，方程y²=x³-2b²+a³無整數解。更一般地，當a≡-1(mod 4)，b≡0(mod 2)，k無平方因子，(k，b)=1，k≡3(mod 4)，k≡2(mod 3)，b0(mod 3)，對每一個奇素數p，勒讓德符號
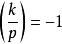莫德爾方程時，p∤(a，b)，這時方程y²=x³+kb²-k³a³無整數解。直到1875年，佩賓(T.Pepin)完整地證明了方程y²=x³-2僅有解(x，y)=(3，±5)。1912年，莫德爾由於給出方程(1)的一系列新結果，榮獲英國劍橋大學頒發的史密斯獎；1918年，他又證明了方程(1)僅有有限組整數解，1930年，內格爾(T.Nagell)證明了方程y²=x³+17的8組正整數解分別是(x，y)=(-2，3)，(-1，4)，(2，5)，(4，9)，(8，23)，(43，282)，(52，375)，(5234，378661)；1968年，貝克證明了方程(1)的整數解滿足
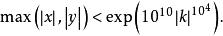莫德爾方程