簡介
艾德曼-外爾斯特拉斯角條件是泛函的極值曲線在其角點處應滿足的條件。
實例
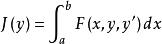 艾德曼-外爾斯特拉斯角條件
艾德曼-外爾斯特拉斯角條件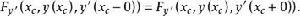 艾德曼-外爾斯特拉斯角條件
艾德曼-外爾斯特拉斯角條件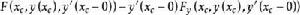 艾德曼-外爾斯特拉斯角條件
艾德曼-外爾斯特拉斯角條件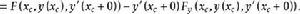 艾德曼-外爾斯特拉斯角條件
艾德曼-外爾斯特拉斯角條件例如,若y=y(x)是泛函 的極值曲線,(x,y(x))是y=y(x)的一個角點,則有
極值曲線
極值是變分法的一個基本概念。
泛函在容許函式的一定範圍內取得的最大值或最小值,分別稱為極大值或極小值,統稱為極值。
使泛函達到極值的變元函式稱為極值函式,若它為一元函式,通常稱為極值曲線。
艾德曼-外爾斯特拉斯角條件(Erdmann-Weierstrass corner condition)是泛函的極值曲線在其角點處應滿足的條件。
艾德曼-外爾斯特拉斯角條件是泛函的極值曲線在其角點處應滿足的條件。
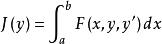 艾德曼-外爾斯特拉斯角條件
艾德曼-外爾斯特拉斯角條件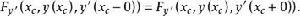 艾德曼-外爾斯特拉斯角條件
艾德曼-外爾斯特拉斯角條件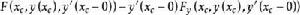 艾德曼-外爾斯特拉斯角條件
艾德曼-外爾斯特拉斯角條件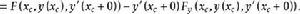 艾德曼-外爾斯特拉斯角條件
艾德曼-外爾斯特拉斯角條件例如,若y=y(x)是泛函 的極值曲線,(x,y(x))是y=y(x)的一個角點,則有
極值是變分法的一個基本概念。
泛函在容許函式的一定範圍內取得的最大值或最小值,分別稱為極大值或極小值,統稱為極值。
使泛函達到極值的變元函式稱為極值函式,若它為一元函式,通常稱為極值曲線。
飾)和萊納德·霍夫斯塔特Leonard Hofstadter (約翰尼...萊爾德悶悶不樂的心情,拉傑回來後把與潘妮的事情說給了大家聽,當然,重點在...泡妞的傢伙,很多時候他的泡妞手法都讓對方感到噁心。來自印度的拉傑什·庫斯...
劇情簡介 分集劇情 演職員表 角色介紹 音樂原聲,失憶了。斯特凡被女巫昆特西亞所救,昆特西亞道出賽拉斯當年背叛了自己,同...瑪拉喝下了永生之水的解藥並殺了她。昆特西亞對斯特凡下咒削弱了賽拉斯,她...還霸占了塞爾瓦托兄弟的大房子。斯特凡和卡洛琳想阻止悲劇的發生,卻也深陷其中...
劇情簡介 分集劇情 演職員表 角色介紹 音樂原聲拉斯的威脅,無奈之下只能向達蒙尋求保護,埃琳娜開始懷疑斯特凡的下落,並且...時,他,失憶了。斯特凡被女巫昆特西亞所救,昆特西亞道出賽拉斯當年背叛...,她逼阿瑪拉喝下了永生之水的解藥並殺了她。昆特西亞對斯特凡下咒削弱了賽拉...
劇情簡介 分集劇情 演職員表 角色介紹 音樂原聲。拉傑根本不敢和這么直接沒禮貌的艾米搭話。回家路上,萊爾德問謝爾頓關於艾...,說到研究方向,艾米明顯得表達出了對其他領悟的鄙視,包括謝爾頓萊爾德拉傑和...納黛特給霍爾德打電話,霍爾德大肆炫耀,萊爾德很尷尬,可是就連拉傑也有...
劇情簡介 分集劇情 演職員表 角色介紹 音樂原聲的前夫所不能給予的,所以她帶著她和前夫所生的孩子曼尼-德爾加多同傑伊-普...脾氣衝著院子裡的爸爸喊叫。盧克用玩具槍打疼了艾麗克斯,克萊爾讓菲爾懲罰盧克...帶著曼尼到克萊爾家裡玩,歌洛莉亞要帶艾麗克斯出去購物,克萊爾說艾麗克斯不...
劇情簡介 分集劇情 演職員表 角色介紹 幕後花絮的前夫所不能給予的,所以她帶著她和前夫所生的孩子曼尼-德爾加多同傑伊-普...。克萊爾和丈夫菲爾依依不捨的將大女兒海莉送入了大學,眼看二女兒艾麗克斯和...院子裡的爸爸喊叫。盧克用玩具槍打疼了艾麗克斯,克萊爾讓菲爾懲罰盧克,讓他...
劇情簡介 分集劇情 演職員表 角色介紹 幕後花絮的前夫所不能給予的,所以她帶著她和前夫所生的孩子曼尼-德爾加多同傑伊-普...。克萊爾和丈夫菲爾依依不捨的將大女兒海莉送入了大學,眼看二女兒艾麗克斯和...的爸爸喊叫。盧克用玩具槍打疼了艾麗克斯,克萊爾讓菲爾懲罰盧克,讓他也嘗嘗...
劇情簡介 分集劇情 演職員表 角色介紹 幕後花絮的前夫所不能給予的,所以她帶著她和前夫所生的孩子曼尼-德爾加多同傑伊-普...的成長,家庭主婦克萊爾和丈夫菲爾的煩惱接踵而至:書呆子二女兒艾麗克斯馬上...。克萊爾和丈夫菲爾依依不捨的將大女兒海莉送入了大學,眼看二女兒艾麗克斯和...
劇情簡介 分集劇情 演職員表 角色介紹 幕後花絮給予的,所以她帶著她和前夫所生的孩子曼尼-德爾加多同傑伊-普里奇特組成家庭...莉亞帶著曼尼到克萊爾家裡玩,歌洛莉亞要帶艾麗克斯出去購物,克萊爾說艾麗克斯不會去的,誰知艾麗克斯說她非常想去,艾麗克斯說媽媽一點也不了解自己。曼...
概述 分集劇情 演職員表 角色介紹 幕後花絮