基本介紹
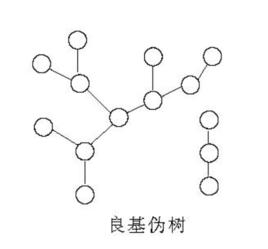
良基關係是集合上的一種重要關係，它是策梅洛(E.F.F.Zermelo)於1935年提出的。設R是集合A上的一個關係，若A的任何非空子集B都有R極小元，則稱R是A的 良基關係。A是關於R的良基集，記為wf(A)。A上的任何良序關係都是A上的良基關係，但A上的良基關係不一定是A上的良序關係。如果A對於關係R不但是良基的，而且是全序的，那么A是良序集，例如，自然數集{1，2，…}對小於關係既是良序的也是良基的，如果有限偏序集的哈塞圖是有分叉的偽樹(如圖1)，則它是良基的但不是良序的。在良基集wf(A)中，不存在無窮的單調遞降序列
{a}：aR aR aR aR …
若定義良基集到序數集內一個映射f：A→ord，使得當a∈A時，
f(a)=sup{f(b)+1|(b∈A∧bRa)}，
且f的值域是一個序數，則f是A到ord內的一個確定單調增映射。f的值域稱為R的長度，即
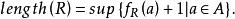良基關係例圖中R的長度為6 。
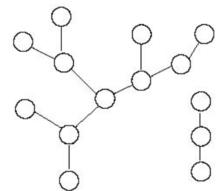圖1 良基偽樹相關定理及其證明
定理 —關係R為良基的的，若且唯若不存在具有定義域為ω的函式f，使得對於每一n∈ω，都有R(f(n )，f(n))。
人們也稱這一序列：
...,f(n ),f(n),...,f(1),f(0) (1)
為一降鏈，並且對於上述f，我們令
D：={f(n)|n∈ω} ， (2)
並稱這一D為f|d(R)的一降鏈子集合。
證明：假定一關係R不是良基的，那么存在一非空集合S，它沒有R極小!元素，亦即
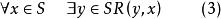良基關係
良基關係
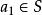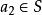良基關係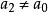
良基關係
良基關係直觀地講，因為S不空，任取 ，由(3)就有a，使得；R(a，a)成立，又由於 ，由(3)就有 ，使得R(a，a)成立。這裡可以取a不同a，因為由S中沒有R的極小元，那么，S=S-{a}中也沒有R極小元，把S套用於(3)即得 ，把這—·過程無限地作下去，即得到下述無窮序列；
a，a，a，... (4)
並且有：對於每一n∈ω，都有
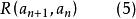良基關係或者記做
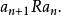良基關係這樣我們可以令：
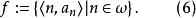良基關係由(5)與(6)，即得欲證結果。
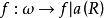良基關係反之，若存在一函式 ，我們令：
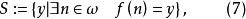良基關係不難證明由(7)給出的集合S中沒有R極小元。
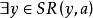良基關係註記：在上述證明中，我們說“把一過程無限地進行下去，即得到下述無窮序列"(指獲得(4)，這句話包含著有無窮多情形，並且在每個種情形下都需要由a去找一個b，使得bRa，我們知道雖然 ，但是(3)並未給出去選擇y的方案。也就是說可能有許多元甚至無窮多元y滿足xRx，根據什麼原則去挑選唯一的元素呢?人們已經證明僅在ZF系統中是不可能實現的，它要求使用選擇公理，不過，這裡僅需用選擇公理的一種較弱的形式稱之為依賴選擇原則，它意味著允許人們依次進行ω次的選擇。
依賴選擇原則(Bernays，1942)：如果T是在不空集合S上的一個關係，使得對於每
一x∈S，都存在y∈S有T(x、y)，那么就存在一序列：
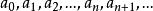良基關係使得
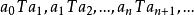良基關係成立。
現在我們令依賴選擇原則中的T(x、y)為
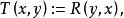良基關係據依賴選擇原則，由(3)即可獲得(4)。
