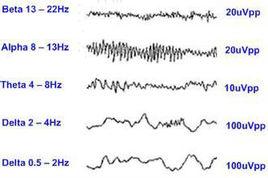
背景簡介
腦電圖(EEG)是腦神經細胞電生理活動在大腦皮層或頭皮表面的總體反映 。腦電信號中包含了大量的生理與疾病信息 ,在臨床醫學方面 ,腦電信號處理不僅可為某些腦疾病提供診斷依據, 而且還為某些腦疾病提供了有效的治療手段。在工程套用方面 , 人們也嘗試利用腦電信號實現腦-計算機接口(BCI),利用人對不同的感覺、運動或認知活動的腦電的不同, 通過對腦電信號的有效的提取和分類達到某種控制目的 。但由於腦電信號是不具備各態歷經性的非平穩隨機信號 ,而且其背景噪聲也很強,因此腦電信號的分析和處理一直是非常吸引人但又是具有相當難度的研究課題。
自 1932 年 Dietch 首先用傅立葉變換進行了 EEG分析之後 ,在腦電分析中相繼引入了頻域分析 、時域分析等腦電圖分析的經典方法。近年來, 在腦電圖分析中套用了小波分析、匹配跟蹤方法 、神經網路分析、混沌分析等方法以及各種分析方法的有機結合 ,有力地推動了腦電信號分析方法的發展 。
腦電信號分析方法
頻域分析
功率譜估計
功率譜分析是 EEG信號處理最常用工具 ,源於傅氏變換 ,它的前提是平穩隨機信號 ,對非平衡隨機信號而言 ,不同時刻的譜分析結果是不同的。目前常用的方法之一是以短時間斷數據的傅氏變換為基礎的周期法 ,具體做法是把實際淮信號在時域上分段 ,並看作是準平穩的 ,每段取傅氏變換後的幅頻特性平方再乘以適當的窗函式 ,作為該信號的功率譜估計 ,但此法頻率解析度差 ,存在邊瓣泄漏 ,譜估計方差大等問題。
腦電信號 ( EEG)是非平穩隨機信號 ,它的頻域特性的正確表達及精度 ,相位信息的提取 ,瞬態波形分析是當前 EEG信號處理研究中的熱點問題。然而由於譜分析方法存在的共同問題是估計的方差特性不好,而且估計值沿頻率軸的起伏比較劇烈 ,數據越長,這種現象越嚴重 。所以提出了參數模型譜估計方法，該方法對數據處理能得到高解析度的譜分析結果 ,從而為 EEG信號頻域特徵的提取提供新的有效手段 ,特別是在動態特性分析中顯示優越性。
AR參數模型譜估計
腦電信號的 AR模型:
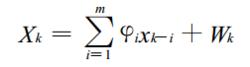腦電信號分析X是腦電信號現實值: φ 是模型參數: m 是模型階數 ;Wk是零均值平穩高斯噪聲。AR模型係數比 MA和 ARM A較易從求解線性方程組或遞推計算中得到 ,模型中研究的隨機信號是平穩白噪聲激勵線性濾波器的輸出。 AR模型首先選擇最佳 階次問題 , 常用的定階準則有信 息論準 則( AIC) ,最終預測誤差準則 ( FPE)等 ,階次確定後按信號數據列與它的估計量之間均方誤差最小準則 ,求取ak 值。 AR係數 的算 法有 Yule-Walker, Burg algorithm , Least Squares等 ,各有利弊。
雙譜分析
功率譜分析可以有效地反映信號的二階信息, 卻丟失了包括相位信息在內的高階信息 , 而這些信息對EEG 信號分析有時顯得很有意義。雙譜密度函式定義為:
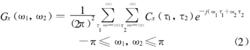腦電信號分析C為平穩隨機過程 x(t)的三階中心矩 。m是 x(t)的均值。雙譜函式只包含了信號的相位信息 ,但未給出相位信息。對於高斯隨機分布而言,雙譜作為隨機信號偏離高斯分布的一個測度, 經過對實際 EEG 數據檢驗表明,不同功能狀態下的 EEG 對高斯分布的偏離度有較大差別。如利用 AR 模型進行雙譜分析。套用三階遞歸(TOR)方法估計雙譜 ,分析局灶性缺血腦損傷 EEG 的特徵 , 可以看到損傷區域的 EEG 雙譜的分布發生變化,在損傷的不同階段,損傷區域與非損傷區域的雙譜最大值以及加權雙譜中心(WCOB)有明顯不同的變化 。
雙譜分析要求信號至少三階平穩 , 因此對短數據EEG 信號才有意義。
時域分析
直接從時域 提取特徵是最早發展起來的方法, 因為它直觀性強, 物理意義比較明確 ,因此仍有不少腦電圖醫生或技師使用。過去的 EEG 分析主要靠肉眼觀察,這可以看作是人工時域分析。時域分析主要用來直接提取波形特徵, 如過零截點分析、直方圖分析 、方差分析 、相關分析、峰值檢測及波形參數分析、相干平均 、波形識別等等 。
時頻分析腦電信號是一種時變的、非平穩信號,不同時刻有不同的頻率成分 ,而單純的時 、頻分析方法通過傅氏變換聯繫起來,它們的截然分開是以信號的頻率時不變特性或統計特性平穩為前提的。但由於時域和頻域解析度的“不確定性原理” , 不可能在時域和頻域同時獲得較高的解析度 。而且在 EEG 中有許多病變都是以瞬態形式表現的, 只有把時間和頻率結合起來進行處理,才能取得更好的結果 。可以說信號的時 -頻表示法為腦電信號處理提供了非常好的前景 。目前套用的較為廣泛的方法有維格納 -費利分布(Wigner -VilleDistribution ,WD)和小波變換 ,匹配跟蹤方法目前也已用於睡眠 紡錘波的分析。
小波變換
小波變換因為具有(1)多解析度(多尺度);(2)品質因數,即相對頻寬(中心頻率與頻寬之比)恆定 ;(3)適當地選擇基本小波 ,可使小波 在時、頻兩域都具有表徵信號局部特徵的能力。當使用較小尺度時, 時軸上觀察範圍小 ,而在頻域上相當於用較高頻率做解析度較高的分析 ,即用高頻小波做細緻觀察;當使用較大尺度時,時軸上觀察範圍大,而在頻域上相當於用低頻小波作概貌觀察。因此小波變換被譽為“數學顯微鏡” 。
人工神經網路(ANN)分析
神經網路是由大量處理單元廣泛互連而成的網路。它反映了人腦功能的基本特性, 是人腦的某種抽象、簡化與模擬 。網路的信息處理由神經元之間的相互作用來實現;知識與信息的存儲表現為網路元件互連間分散式的物理聯繫 ;網路的學習和識別決定於各神經元連線權係數的動態演化過程。神經網路可用作自發腦電(EEG)分析 , 分析的目的是為了檢測 EEG 尖波和癲癇發作, 輸入方式可以使用原始信號模型和特徵參數模型。目前有利用小波變換和人工神經網路相結合的方法來檢測 EEG 信號中的棘波和尖波成分 。利用小波變換 (WT)對基於ANN的EEG 棘波檢測系統的輸入進行預處理 ,從而在不減少信號的信息內容和降低檢測性能的前提下減少ANN 的輸入規模 。
非線性動力學分析
近年來,隨著非線性動力學的發展 ,越來越多的證據表明大腦是一個非線性動力學系統 , 腦電信號可以看作是它的輸出 。因此人們嘗試把非線性動力學的一些方法,如分維數、Lorenz 散點圖、Lyapunov 指數 、複雜度等用於腦電信號分析, 以期獲得對大腦的新的認識 。腦電信號的 Lorenz 散點圖是指以腦電信號相鄰兩採樣點的前一點值為橫坐標, 後一點值為縱坐標繪製而成的圖 。資料表明 ,癲癇病人腦電信號相鄰採樣點的值較為接近且整段腦電信號的值的分布範圍較大, 而正常人腦電信號的Lorenz 散點圖中的點大多分布在一個範圍較小的橢圓形區域 。
初步研究表明, 腦電動力學特性表現出極強的科學性和套用價值 ,它從物理學思想出發 ,提供了常規分析方法所無法得到的信息 ,具有不受特殊點影響和可重複性的優點。
結語
腦電信號是明顯的非平穩性信號, 從20 年代檢測到腦電信號 以來 ,雖然已作了大量的工作,但長期以來還沒有突破性的進展 。隨著信號處理方法 的不斷發展,更多更有效的分析方法在腦電信號分析中的套用,人們對於腦電活動機理 將有進一步的認識 , 也必將為臨床醫學和基礎醫學的發展作出新的貢獻。
