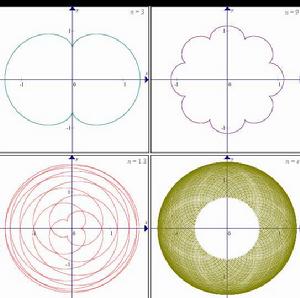
定義
外擺線是所有形式為
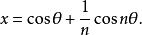 腎臟線
腎臟線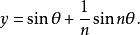 腎臟線
腎臟線的曲線,其中n為正實數。
腎臟線亦是外擺線的一種,其n為3。
軌跡定義
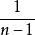 腎臟線
腎臟線假設有一個定圓,若有另一個半徑是剛才的圓形的 倍的圓在上滾動,則圓周上的一定點在滾動時劃出的軌跡就是一條外擺線。
內擺線
定義:當半徑為b的圓沿著半徑為a(a>b)的圓的內側無滑動滾動時,動圓圓周上一點p的軌跡。
在以定圓中心為原點的直角坐標系中,其方程為
X=(a-b)cosθ+bcos[(a-b)θ/b],Y=(a-b)sinθ-bsin[(a-b)θ/b]。
心臟線
心臟線是外擺線的一種,其n為2。它亦可以極坐標的形式表示:
r= 1 + cosθ;
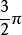 腎臟線
腎臟線這樣的心臟線的周界為8,圍得的面積為 。 心臟線亦為蚶線的一種。
在曼德博集合正中間的圖形便是一個心臟線。心臟線的英文名稱“Cardioid”是de Castillon在1741年的《Philosophical Transactions of the Royal Society》發表的;意為“像心臟的”。