基本介紹
羅吉特生命表系統即羅吉特變換值。英國人口學家布拉斯發展的一個十分靈活的模型生命表。布拉斯於1966年提出了一種思想,用數學變換將兩個不同的生命表聯繫起來,他發現,兩個不同生命表的存活機率之間存在近似關係:λ(l)=α+βλ(t) —— (1),式中,l,t分別為兩個生命表的x歲的存活機率,λ(l)為l的羅吉特變換,λ(x)=0.5ln((1-x)/x)。這樣,通過改變α和β,任何一張生命表的羅吉特變換都可以用某一標準生命表羅吉特變換的線性函式近似表示出來,進而編制生命表。布拉斯的羅吉特生命表系統沒有給出固定的一套若干張生命表,只給出了一個標準的羅吉特變換值,套用時根據公式(1),變換α和β的值即可得到需要的生命表。布拉斯的羅吉特生命表系統的優點是簡單、靈活,並容易在計算機上進行調整、分析,但他給出的標準表並不能很好對任何實際生命表通過公式(1)來表示,實際上也不存在這種標準表。因此,在使用羅吉特生命表系統時,最好先根據已有資料和經驗,選取與所研究人口的死亡模式大致相近的生命表作為標準表,以降低誤差。
相關介紹
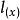 羅吉特生命表系統
羅吉特生命表系統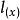 羅吉特生命表系統
羅吉特生命表系統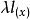 羅吉特生命表系統
羅吉特生命表系統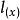 羅吉特生命表系統
羅吉特生命表系統布拉斯和他的同事提出了一套靈活性的模型生命表。這就是著名的羅吉特(logit)模型生命表。布拉斯試圖用數學的方法將兩個不同的生命表聯繫在一起。他發現,將0歲至x歲的存活機率(在生命表中為 )進行某種變換後,兩個不同生命表上的存活機率 之間存在一種近似的線性關係。換句話說,如果讓 代表對 值的某種變換,則線性關係為:
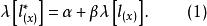 羅吉特生命表系統
羅吉特生命表系統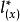 羅吉特生命表系統
羅吉特生命表系統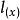 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統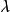 羅吉特生命表系統
羅吉特生命表系統這裡 和 是兩張不同生命表上從0歲至x歲的存活機率; 和 是兩個係數,如果把 定義為:
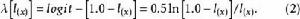 羅吉特生命表系統
羅吉特生命表系統那么對所有x值來說,(1)的線性關係差不多是真實存在的。
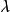 羅吉特生命表系統
羅吉特生命表系統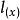 羅吉特生命表系統
羅吉特生命表系統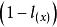 羅吉特生命表系統
羅吉特生命表系統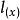 羅吉特生命表系統
羅吉特生命表系統那么熟悉統計學中羅吉特定義的人注意到, 正好是此函式的特例,它是用 的補數 代替 本身計算出來的,統計學中,機率P的羅吉特為:
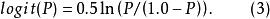 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統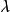 羅吉特生命表系統
羅吉特生命表系統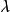 羅吉特生命表系統
羅吉特生命表系統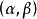 羅吉特生命表系統
羅吉特生命表系統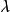 羅吉特生命表系統
羅吉特生命表系統假定對於每兩張生命表,如果能找到 和 的值,並由此得到方程(1),便可以證明任何一張生命表的 變換都可以用某一“標準”的生命表 變換的線性函式表達出來。也就是說,如果方程(1)對每對生命表均成立,那么所有的生命表都可以從一張生命表中通過改變 值推導出來。事實上,方程(1)並不是完全成立。兩張生命表存活機率的 變換之間,只是存在一種近似的線性關係,但這種近似的程度已足夠人們用這種線性假設去研究和擬合實際的死亡率。
 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統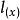 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統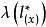 羅吉特生命表系統
羅吉特生命表系統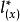 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統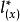 羅吉特生命表系統
羅吉特生命表系統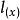 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統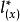 羅吉特生命表系統
羅吉特生命表系統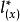 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統在描述方程(1)如何產生模型生命表之前,首先應該解釋一下參數 和 的含義。通過選擇一個特定的生命表 並計算出不同 和 值所得到的 ,可以產生生命表 。如果令 為一常數並等於1,不斷使 值變化, 曲線的形狀與 的相同,而其水平則發生了變化(見圖1)。反之,如果 值保持不變,不斷使 值發生變化, 曲線的形狀將不斷發生變化。所有 曲線在年齡中段某一處交於一點,因此,存活機率或者在年輕組較高,在老年組較低;或者在年輕組較低,在老年組較高。故改變 值對死亡率曲線形狀的影響遠遠大於對其水平的影響。當然,如果同時變化 和 值,所產生的死亡率曲線的形狀和水平則都將發生變化。
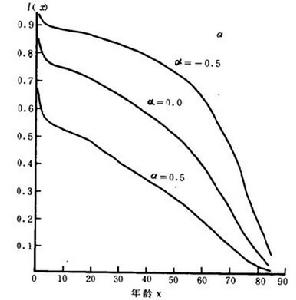 圖1 當β=1.0時,用布拉斯一般標準生命表得出的存活機率曲線
圖1 當β=1.0時,用布拉斯一般標準生命表得出的存活機率曲線從方程(1)和(2)可以推導出如下公式:
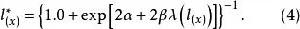 羅吉特生命表系統
羅吉特生命表系統 圖2 當α=0.0時用布拉斯一般標準生命表得出的存活機率曲線
圖2 當α=0.0時用布拉斯一般標準生命表得出的存活機率曲線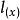 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統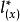 羅吉特生命表系統
羅吉特生命表系統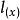 羅吉特生命表系統
羅吉特生命表系統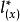 羅吉特生命表系統
羅吉特生命表系統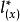 羅吉特生命表系統
羅吉特生命表系統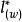 羅吉特生命表系統
羅吉特生命表系統因此,只要確定一套生命表的 值,用任意一對 和 的值就可以獲得另外一套 值。(注意,在年齡組的首末兩端點, 值分別是1與0,方程(4)不能用來計算 。倒不如人為地規定 和 分別等於1和0)。通過選擇適當的標準生命表,方程(4)即可用來建立模型生命表。從理論上說,任何生命表都可作為標準生命表,但是為了便於模擬和擬合,常用布拉斯提出的一般標準生命表。布拉斯提出的“一般標準”不同於所謂“非洲”標準,非洲標準是:嬰兒死亡率低;兒童死亡率高。
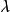 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統由於方程(2)和(4)數學上很簡單,用 變換(以後也叫“羅吉特”變換)導出模型生命表,並不需把所得的數值結果列印出來。然而,的確有這樣的值區被列印。例如,卡里(Carrier)和霍伯別羅夫特(Hobcraft)通過 的值確定為1,用非洲標準生命表製做了一套模型生命表。因此,這種模型生命表代表了一個單參數模型生命表系統。
 羅吉特生命表系統
羅吉特生命表系統 羅吉特生命表系統
羅吉特生命表系統方程(4)以簡單的數學函式表達生命表,使其在計算機中的套用也得到了簡化。由於這個原因,羅吉特模型生命表產生的生命表經常被用來做模擬分析。此外,羅吉特模型特別適合用來做死亡率預測。如果已知某人口的過去和現在的死亡率曲線,通過使用羅吉特模型生命表系統擬合每個死亡率曲線,就可以確定 和 參數的趨勢。這種趨勢還可謹慎地用來預測未來的死亡率。