基本概念
可行解
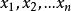線性規劃圖解法把滿足約束條件的一組決策變數值 稱為該線性規劃問題的可行解。
可行解集/可行解域
滿足約束條件的可行解的全體稱為可行解集。
在平面上，所有可行解的點的集合稱為可行解域。
最優解
在可行解集中，使目標函式達到最優值的可行解稱為最優解。
一般步驟
1、建立數學模型。
2、繪製約束條件不等式圖，做出可行解集對應的可行解域。
3、畫目標函式圖。
4、判斷解的形式，得出結論 。
舉例
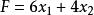線性規劃圖解法（1）求 的最大值。
約束條件：
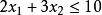線性規劃圖解法
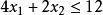線性規劃圖解法
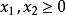線性規劃圖解法（2）繪製可行解域：
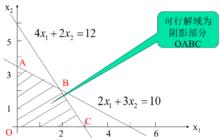線性規劃圖解法（3）畫目標函式圖：
令目標函式值為零，可得到斜率，根據斜率做一過原點的直線。（如果可行解域在第一象限，且目標函式等值線斜率為負）若給出問題是求最大值，把目標函式等值線平行移動到與可行解域最後相交的點，這點就是問題的最優解；若給出問題是求最小值，把目標函式等值線平行移動到與可行解域最先相交的點，這點即為問題的最優解。
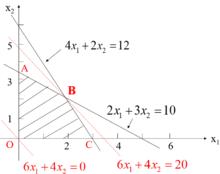線性規劃圖解法（4）判斷解的形式，得出結論。
本題有唯一的最優解。
解法：
最優解是由兩根直線所確定的最後的交點；
解由此兩根直線相應方程所組成的方程組，得到問題的精確最優解；
將最優解代入目標函式，得最優值。
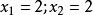線性規劃圖解法將最優解代入目標函式，得最優值：
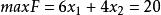線性規劃圖解法