網路路由的概念
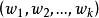 網路路由
網路路由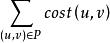 網路路由
網路路由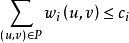 網路路由
網路路由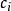 網路路由
網路路由給定網路G(V,E),V是節點集,V =N,E是邊集,E =M。P是路徑集對源節點S∈V及目的節點T∈V,找一條從S到T的路徑p∈P,使得開銷最小,而所有約束都能滿足。設對每一個邊(u,v)∈E,有損失函式cost(u,v)及權向量 ,則要求最小化 滿足約束 , 是常數,0≤i<k。
下一代高速廣域網對實時流要求面向連結的路由。在運輸層連結(呼叫)意味著終端用戶之間的邏輯聯繫及正確有序的數據投遞。在網路層,連結意味著一條包含開關和鏈路的網路路徑。同一連結的數據包沿路徑按先進先出(FIFO)順序傳送。基於服務質量路由的約束包括鏈路約束、路徑約束、樹約束、時延約束等,而頻寬則包括鏈路頻寬及CPU頻寬(節點把數據泵到鏈路上的最大速率)。
解這一問題的基礎算法是Dijkstra算法和Bellman-Ford算法。Dijkstra算法是圖論中尋找最短路徑的算法,它實際上求出從源節點到系統中所有節點的最短路徑。把它套用到網路路由,就嫌有點浪費,因為網路路由只要求從源節點到目的節點的最短路徑。Bellman-Ford算法是尋找最短路徑的分散式算法,允許邊的權是負的,看來適合網路路由。但是,各節點的同步是一個問題。在不同步的情況下就可能得不到最優解。
網路路由的分類
網路路由有多種分類。
按網路性質
按網路性質可分為多計算機系統路由、有線網路路由和無線網路路由。計算機系統路由針對一種特定的拓撲結構,例如超立方體、格線,在某些節點或鏈路故障的情況下尋找最優通路。這些想法實質上與網際網路的路由非常類似。但是,今天,一個多計算機系統也許是一個超級大型機,用乙太網連線。再考慮到任意的拓撲結構,問題就更複雜了。
按通信方式
網路路由按通信方式分,可以分為單播路由(即端到端的路由)、多播路由(即端到目的節點集中的每一個節點的路由)及Anycast路由(即端到目的節點集中的任一個節點的路由)。
按路由算法
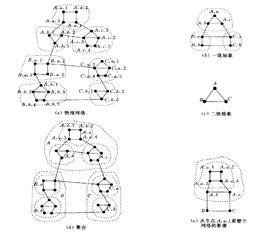
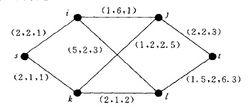 圖1 網路狀態
圖1 網路狀態網路路由按路由算法來分,可以分為源路由算法、分散式路由算法和分級路由算法。
(1)源路由算法假定每個節點了解整個網路的全局狀態。全局狀態用鏈路狀態協定通過廣播獲得,或用距離向量協定,用鄰節點周期性交換距離向量獲得。當要傳送訊息時,源節點就決定了整條路徑。
 圖2 節點S在距離向量下的全局狀態
圖2 節點S在距離向量下的全局狀態(2)分散式路由算法假定每個節點只了解它的鄰節點的情況,即網路局部狀態,包括排隊延遲、傳播延遲、剩餘頻寬等,根據路徑的要求,只決定下一跳應走向哪裡(見例1)。
例1:考慮圖1的網路,鏈路狀態由(頻寬、時延、花費)給定。圖2給出了節點S在距離向量下的全局狀態。
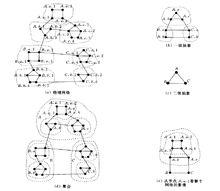 圖3 分級網路
圖3 分級網路(3)分級路由算法假定網路節點分級,每個節點了解聚合的全局狀態,即自己所在範圍內的情況,而對遠處的上級節點只了解大致情況。即每一物理節點保持聚合的網路影像(見例2)。
例2:圖3給出一個分級網路模型。圖(a)表示一個實際的網路,有29個節點;圖(b)示出其第一級節點,共7個;圖(c)示出第二級節點共3個,該物理網路經過聚合可以變成圖(d);而從節點A、a、1來看整個網路則如圖(e)所示。
按對路由的要求
網路路由按對路由的要求來分,可以分為盡力而為路由和基於服務質量路由。盡力而為路由是面向連線或帶動態性能的無連線,以保證公平性、總吞吐量和平均回響時間為目標,在當前的網路環境下來選擇最優路徑。而基於服務質量的路由是對各流的包基於服務質量要求選擇可用路徑的過程,它面向連線,帶資源預留,以滿足各流的連線要求,減少呼叫阻塞。因此,它著重在滿足約束,希望連線的數據傳輸不受其它連線的動態流量的影響。問題是網路永遠是動態的,節點對全局網路服務質量狀態的了解不精確、不實時,對路由的確定與預計就未見得完全正確。服務質量路由的代價主要包括兩方面:一方面是計算開銷。因為它需要更加複雜和頻繁的路由計算。另一方面則是協定開銷,因為它要分散式地提供和刷新與路由選擇有關的網路資源狀態信息。
路由選擇計算
何時進行路由選擇計算?一般來說是當每一次請求來到時觸發路由選擇。但是,如果在兩次狀態刷新之間,收到許多請求,也許事先計算好路由更加有效。當然也可以在收到狀態刷新信息時計算路由。同時,路由選擇必須有靈活性,以免由於路由而造成某些路徑擁塞、某些路徑又很空閒。狀態刷新的觸發也可以選擇不同的時機。譬如現在的狀態比原來變化超過50%就觸發刷新,或者是,將可用頻寬按大小分級,跳了一級就觸發刷新。也可以周期性地定時觸發。刷新內容包括刷新訊息的大小、通報的指標值的類型等都要在協定中規定。各種刷新方案各有優劣。刷新越及時,路由需要的網路狀態信息就越精確,但刷新太頻繁,增加網路負擔。要在兩個極端中折衷。在IPv6協定環境下,更多的地址和報頭信息也會有助於網路路由。
單播路由算法
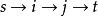 網路路由
網路路由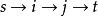 網路路由
網路路由單播路由是指目的節點只有一個的路由。以剩餘頻寬和剩餘快取空間為服務質量目標的路由選擇是一類基於鏈路信息的路由,所選路徑一般是根據路徑上的瓶頸鏈路狀態來決定的。例如圖1中路徑 的頻寬是1,因為其瓶頸鏈路(i,j)的頻寬是1。這一類路由可分為鏈路最優路由和鏈路約束路由。這兩類基本路由問題可以用Dijkstra或Bellman-Ford多項式複雜性的算法解決。另一方面,以時延、時延抖動和花費為服務質量目標的路由選擇是另一類所謂基於路徑信息的路由。例如圖1中 的路徑時延是10,它是路徑上各鏈路時延之和。從而引出另外兩類基本路由問題:路徑最優路由和路徑約束路由。它們也可以用多項式複雜性的算法解決。
對於許多實際套用,路由不但對鏈路有要求,也對路徑有要求,或者是對鏈路有多個要求,或者對路徑有多個要求。例如最寬約束最小時延路由就是要求瓶頸鏈路最寬,而且路徑時延最小。又如頻寬約束和快取約束路由,如此等等,可以派生出許多組合的路由問題。其中只有兩類有意義的NP難問題,即路徑約束路徑最優路由(PCPO)和多路徑約束路由(MPC)。譬如時延約束最小花費路由,時延和時延抖動約束路由。若所有指標(除一個以外)全有界,或者全相關,則多項式時間可解。否則,這兩類問題是NP難的。典型的單播路由算法有:
源路由算法
如果路由既有頻寬約束,又有時延約束,源路由算法的複雜性就會增加。
分散式路由算法
分式式路由算法把源路由算法的計算開銷分散到各個節點上,各個節點只需要了解局部的信息,作出局部的路徑決策。這個算法一般用來找最短的最寬路徑(瓶頸頻寬最大的路徑),但當不同節點的狀態信息有矛盾時,該路由算法可能產生循環路由。
分級路由算法
當今網際網路的顯著特徵是大型,而且天天在變化。分級路由恰恰是用來解決大型互連網源路由可擴展性問題的。對於ATM網路由的專用網路間接口標準(PNNI)就是分級的,每一個節點只保存一部分全局狀態,許多節點集被聚合為邏輯節點。所以,這種聚合的全局狀態的大小不過是整個全局狀態大小的對數。因此,分級路由算法既能保持某些源路由算法的優點,又有許多分散式路由算法的優越性。因為路由計算由許多節點承擔,分級路由算法先從源節點的聚合全局狀態出發,從最高層開始逐步下走,直到第一層。確定了源節點所在最高層節點內的路由之後,交給下一個最高層節點的邊界節點去確定在其內的路由,如此等等,直到目的節點。不難想像,路由算法的這種簡化,必然帶來路由質量的代價。聚合信息的不精確性嚴重影響路由的質量。考慮圖3(e),很難估計從A、a、1到C中節點的時延,因為C的內部結構被隱藏了,並且,從A、c中的不同的節點到C中不同節點的時延可以是很不相同的,但在聚合的狀態中只有一個時延值。所以,基於聚合信息的時延值是很不精確的。如果有多個服務質量約束,問題就更複雜。
按比例路由
選最短路徑可以最小化資源利用,但這些被選路徑由於常常被選上,而負載過重。選最輕負載路徑可以平衡網路負載,但可能不是最短路徑,因而浪費更多資源。另外,要求網路中節點保持精確的實時的服務質量狀態是不現實的。事實上,保持精確的實時的服務質量狀態只能靠及時更新,目前無法靠預測。更新時間太長,所得狀態不精確;太短,開銷又太大。選擇最好路徑還有同步的問題,一次刷新以後,空閒的鏈路會擁塞,而再一次刷新以後又會變得空閒。
基於策略的路由
邊界網關協定(BGP)是網際網路域間路由協定。它允許自治系統獨立地定義自己的路由策略,這就給網路路由提供了個性和靈活性。但是,同時也產生穩定性和收斂性的問題。有例子指出,基於策略的路由可能產生循環路由和路由振盪,這已經不光是一個路由的問題,還是一個協定的問題。
多播路由算法
多播路由的問題是:給定源節點S和目的節點集R、約束集C,也許還有一個最優目標,求最好的可行樹,覆蓋s和R的所有節點,滿足約束C。例如在多播情況下,頻寬最優的路由要求樹的瓶頸鏈路頻寬最大,時延約束路由則要求從傳送者到所有目的節點的端到端延遲都小於一個給定值。
著名的斯坦(Steiner)樹問題就是找花銷最小的樹,也就是最小花銷多播路由問題。帶約束的斯坦樹問題也就是時延約束最小花銷多播路由問題。這都是NP難的。時延和時延抖動雙約束的多播路由問題也是NP難的。只有當所有指標(除一個以外)全有界,或者全相關,才會有多項式時間可解。
多播的源路由算法基於多播鏈路狀態協定(MOSPF),該協定是單播鏈路狀態協定(OSFP)的擴展。每一節點除了保存全局狀態之外,還保存路由域內每一個多播組的成員信息。從而使最短路徑多播路由可用Dijkstra算法解決,時延約束多播路由問題也較容易解決。