定義
如果符合定義，將如下所示：
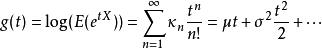累積量生成函式。
將累積量生成函式g(t)對t等於零之處微分
累積量生成函式與機率分布的動差值有很強的關聯性。假如隨機變數X存在期望值μ =E(X)及變異數σ=E((X− μ))，則累積量生成函式g(t)的一階與二階微分剛好是上述數值：μ = κ1及σ= κ2。第c個累積量表達的方式為
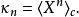累積量生成函式使用累積量生成函式優於動差值的情況在於獨立變數X和Y，
如此一來相加累積量的合可表達成累積量的相加，也就是具有加成性。
一個分布的累積量κn可以使用Edgeworth series來近似。
有些作者偏好定義累積量生成函式為對特徵函式取自然對數，或者有人稱為第二特徵函式，
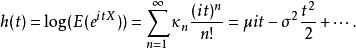累積量生成函式使用此函式的好處在於，即便可能隨機變數X是一大變數仍被完整定義。儘管他的累積量生成函式或者是動差母函式是存在的，但在這種情況下，通常不允許被展開成累積量生成函式或者是動差母函式而表達成線性級數數列的模式。Cauchy distribution（也稱作Lorentzian）和stable distribution（與“Lévy distribution”有關）是生成函式無法被展開的兩個例子。
一些離散隨機變數的累積量
•退化的隨機變數X=1的累積量生成函式為g(t)=1.第一累積量為κ1=g'(0) =1，其他的累積量為零，κ2= κ3= κ4= ... =0.
•退化的隨機變數X=μ.每一個累積量是退化的隨機變數X=1的μ倍。其積量生成函式為g'(t)=μ. 第一累積量為κ1=g'(0)=μ，其他的累積量為零，κ2= κ3= κ4= ... =0.
•伯努利分布，特殊情形為p=1時是退化的隨機變數X=1.累積量生成函式為g'(t) = ((p−1)·e+1)。第一累積量為κ1=g'(0) =p，κ2=g''(0) =p·(1 −p).其累積量可以整理成下面形式
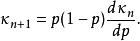累積量生成函式幾何分布，累積量生成函式為g'(t) = ((1 −p)·e−1)。第一累積量為κ1=g'(0)=p−1，κ2=g''(0)=κ1·p.代換p=(μ+1)可得g'(t) = ((μ+ 1)·e−1)及κ1=μ.
•泊松分布，累積量生成函式為g'(t)=μ·e.所有的累積量均為：κ1=κ2=κ3=...=μ.
•二項分布，其特殊情形是n=1時為伯努利分布。每一累積量是n倍相對應的伯努利分布。累積量生成函式為g'(t)=n·((p−1)·e+1)。第一累積量為κ1=g'(0)=n·p及κ2=g''(0)=κ1·(1−p)。代換p=μ·n可得g'(t) = ((μ−n)·e+n)及κ1=μ。極限值逼近情形則為n=0之卜瓦松分布。
•負二項分布，其特殊情形為n=1時是為幾何分布。每一累積量是n倍相對應的幾何分布。累積量生成函式為g'(t)=n·((1−p)·e−1)。第一累積量為κ1=g'(0)=n·(p−1)，及κ2=g''(0)=κ1·p.代換p=(μ·n+1)可得g'(t) = ((μ+n)·e−n)及κ1=μ.比較二項分布與本公式可以知悉負二項分布名字的由來。極限值逼近情形則為n=0之卜瓦松分布。
