簡介
算術溢出(arithmetic overflow)或簡稱為溢出(overflow)指的是:在計算機領域裡所發生的溢出條件是,運行單項數值計算時,當計算產生出來的結果是非常大的,大於暫存器或存儲器所能存儲或表示的能力限制。在計算機領域裡,運行多項或累計的數值計算時,當計算產生出來的總值是非常大的,大於暫存器或存儲器所能存儲或表示的能力限制。要注意的是,溢出可能會在其他地址被置換。
加法器是中央處理器算術邏輯單元中的核心之一。當長度為n位的兩個二進制數經過加減法器運算,得到的長度為n位的結果不是正確值時,我們說發生溢出。
算術下溢
算術下溢也稱為浮點數下溢,是指計算機浮點數計算的結果小於可以表示的最小數。算術下溢在計算結果很接近零出現,使得計算結果的大小小於浮點數可以表示的最小數字。算術下溢也可以視為是浮點數指數在負值時的溢位。例如,浮點數指數範圍為-128至127,一個絕對值小於2−127的浮點數就會造成下溢(假設-128的階碼用於表示負無窮)。界於−fminN and fminN之間的區間稱為下溢間距(underflow gap),其中fminN為一般浮點數格式所能表示的最小正數。
在早期的設計中,界於下溢間距之間的數字其值均視為零,因此若出現算術下溢,其結果會被改為零,可能是用硬體或系統軟體處理,此處理方式稱為“清洗為0”(flush to zero)。
1984年版的IEEE 754導入了次正規數,次正規數和零可以填滿下溢間距。假設浮點數指數範圍為-128至127,最小可表示正規數為2^−127,次正規數則是類似0.9^−127、0.8^−127……之類的數,計算時會將結果轉換為最接近的次正規數,因此可以漸近下溢,不過最接近的次正規數中仍有可能是零。
出現算術下溢時,可能會設定一個狀態位元、產生異常、產生中斷或是這幾項的組合。
IEEE 754中規定只有算術下溢會造成精確度下降時才回報算術下溢,一般是在最後的計算結果不對時才會出現。但若程式要捕捉算術下溢,不論是否有精確度,都會回報算術下溢。IEEE 754處理算術下溢及其他異常的方式相同,都要紀錄算術下溢時的浮點運算器狀態。
控制溢出
有幾個控制溢出的方法:
設計:選擇正確的數據類型,尤其要注意數據長度與signed/unsigned數據符號。
迴避:事先注意指令的運作以及檢查運算的數值,或許可以確保計算出來的結果不會超過存儲器存儲數據的限制。
控制:當它被偵測到,還有在其他的程式完成時被檢測出來,那么溢出是可以被預料的。例如:兩個比特大的兩個數值做加法計算,這種情形最可能發生,步驟如下:先加低比特再加高比特,但是如果它必須完成低比特的運算,就會產生比特加法的運算溢出,那么就有必要做偵測和增加高比特的總和。通常CPU有支持偵測數值加法大於暫存器大小的作法,基本上這個作法是採用狀態比特的方式。
增值:假如存儲的數值過大就會被分配給其他特定的數值,這時溢出就會發生,然後傳回旗標值時就會產生連續運作的現象。檢查這個問題最有用的方法,就是在整體的計算結尾做一次性的檢查工作,而不是檢查每一個運行步驟。這個作法最常用在浮點硬體調用浮點運算器。
忽略:這是最普遍的作法,但是這個作法會得出不正確的結果,以及降低程式的安全性。
1.設計:選擇正確的數據類型,尤其要注意數據長度與signed/unsigned數據符號。
2.迴避:事先注意指令的運作以及檢查運算的數值,或許可以確保計算出來的結果不會超過存儲器存儲數據的限制。
3.控制:當它被偵測到,還有在其他的程式完成時被檢測出來,那么溢出是可以被預料的。例如:兩個比特大的兩個數值做加法計算,這種情形最可能發生,步驟如下:先加低比特再加高比特,但是如果它必須完成低比特的運算,就會產生比特加法的運算溢出,那么就有必要做偵測和增加高比特的總和。通常CPU有支持偵測數值加法大於暫存器大小的作法,基本上這個作法是採用狀態比特的方式。
4.增值:假如存儲的數值過大就會被分配給其他特定的數值,這時溢出就會發生,然後傳回旗標值時就會產生連續運作的現象。檢查這個問題最有用的方法,就是在整體的計算結尾做一次性的檢查工作,而不是檢查每一個運行步驟。這個作法最常用在浮點硬體調用浮點運算器。
5.忽略:這是最普遍的作法,但是這個作法會得出不正確的結果,以及降低程式的安全性。
檢查溢出
大多數的計算機都可以區別以上兩種溢出條件。當加法或減法的結果發生進位,必須考量到當運算的數值與結果都是unsigned numbers(無號數值,即“正數”)類型時,運算的結果就不適合使用這個數值類型。所以,在運行無號數值(正數)的加法或減法之後檢查進位旗標是非常有用的作法。“溢出”在運算結果為無號數值時容易發生,可以從有符號的運算數值預計出這類的情形(例如:兩個正整數相加產生的結果為一個負數)。所以,在運行2的補數的加法或減法之後檢查溢出旗標是非常有用的作法(換言之,有考慮到有號數值)。
定義A和B都是長度為n位的二進制數
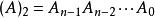 算術溢出
算術溢出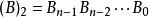 算術溢出
算術溢出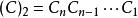 算術溢出
算術溢出以下是豎式(第一行為進位):
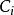 算術溢出
算術溢出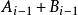 算術溢出
算術溢出其中是的進位
1、輸入的數是無符號整數,我們通過觀察C判斷是否溢出
a) C=1
i)如果是加法操作,結果不正確,結果溢出
ii)如果是減法操作,結果正確,結果未溢出
b) C=0
i)如果是加法操作,結果正確,結果未溢出
ii)如果是減法操作,結果不正確,結果未溢出。在這種情況下,結果是負數。然而,在無符號整數世界裡,負數不存在,我們認識這樣的操作是非法的。當然,如果認為答案是以有符號整數補碼的形式出現,則結果正確。
2、輸入的數是有符號整數,我們通過觀察V判斷是否溢出
a) V=1,結果不正確,結果溢出
b) V=0,結果正確,結果未溢出

