等角橫切橢圓柱投影

等角橫切橢圓柱投影在一般書中稱之為高斯一克呂格投影，簡稱高斯投影。這種投影從幾何方面來說，假想有一個橢圓柱面套在地球橢球的外面，並與某一子午線相切（此子午線叫中央子午線或中央經線），橢圓柱的中心軸通過地球橢球的中心，然後用一定的條件（即等角條件），將中央子午線東西兩側各一定經差範圍內的地區投影到橢圓柱面上，並將此柱面展成平面，即得本投影。

釋義

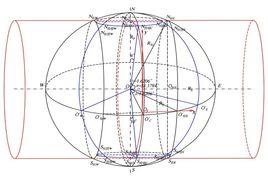
等角橫切橢圓柱投影（transverse elliptic cylindrical equalangle projoction）又名高斯一克呂格投影，簡稱高斯投影。是德國數學家高斯（Carl Friedrich Gause）所創造，後經德國大地測量學家克呂格（Johannes Krilger）加以補充，故名。

投影原理

它是一種正形地圖投影。即假想用一個橢圓柱切於地球橢球體的某一經線（稱為中央經線），將中央經線兩側一定寬度的橢球面按等角條件用數學方法將經緯線投影到橢圓柱面上，再將橢圓柱面切開展成平面。中央經線和赤道在平面上成正交的直線，作為此投影的座標軸，其交點作座標原點。為控制長度變形不超過地圖圖解精度的範圍，首先按一定的經差將地球表面分為若干帶，一般是將中央經線左右各3º（或1.5º）劃分為一帶，稱為六度帶（或三度帶），然後分帶進行投影。

套用

用這種投影方法，在計算國家三角點（導線點）的直角座標時，都在六度帶內進行，在一萬分之一和更大比例尺測圖時，則在三度帶內進行。我國現施測的地形圖即採用這種投影。