立體幾何[數學]
數學上,立體幾何(Solid geometry)是3維歐氏空間的幾何的傳統名稱—- 因為實際上這大致上就是我們生活的空間。一般作為平面幾何的後續課程。立體測繪(Stereometry)處理不同形體的體積的測量問題:圓柱,圓錐, 錐台, 球,稜柱, 楔, 瓶蓋等等。 畢達哥拉斯學派就處理過球和正多面體,但是稜錐,稜柱,圓錐和圓柱在柏拉圖學派著手處理之前人們所知甚少。尤得塞斯(Eudoxus)建立了它們的測量法,證明錐是等底等高的柱體積的三分之一,可能也是第一個證明球體積和其半徑的立方成正比的。
基本課題
課題內容
 各種各樣的幾何立體圖形
各種各樣的幾何立體圖形 包括:
- 面和線的重合
- 二面角和立體角
- 方塊,長方體,平行六面體
- 四面體和其他稜錐
- 稜柱
- 八面體,十二面體,二十面體
- 圓錐,圓柱
- 球
- 其他二次曲面:迴轉橢球,橢球,拋物面 ,雙曲面
公理:
立體幾何中有4個公理
公理1 如果一條直線上的兩點在一個平面內,那么這條直線在此平面內。
公理2 過不在一條直線上的三點,有且只有一個平面。
公理3 如果兩個不重合的平面有一個公共點,那么它們有且只有一條過該點的公共直線。
公理4 平行於同一條直線的兩條直線平行。
常見立體圖形表面積和體積一覽表
| 名稱 | 符號 | 表面積S | 體積V |
| 正方體 | a——邊長 | S=6a² | V= a |
| 長方體 | a——長 b——寬 c——高 | S=2ab+2bc+2ac | V=abc |
| 稜柱 | S——底面積 h——高 | | V=Sh |
| 稜錐 | S——底面積 h——高 | | V=1/3Sh |
| 稜台 | S1和S2——上、下底面積 h——高 | | ![立體幾何[數學]](/img/f/d66/nBnauM3X3gjM3MDOyITM0MjM2UTM1QDN5MjM5ADMwAjMwUzLyEzL0QzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 立體幾何[數學] 立體幾何[數學] |
| 圓柱 | r——底面半徑 h——高 | S=2πrh+2πr² | ![立體幾何[數學]](/img/4/cb5/nBnauM3XwEjNwYjMxgDNxMDN0UTMyITNykTO0EDMwAjMwUzL4QzLzAzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 立體幾何[數學] 立體幾何[數學] |
| 圓錐 | r——底半徑 h------高 l ——母線 | S=πrl+πr² | ![立體幾何[數學]](/img/1/72b/nBnauM3X2cjN4cTM1IzM0IDN0UTMyITNykTO0EDMwAjMwUzLyMzL2gzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 立體幾何[數學] 立體幾何[數學] |
| 圓台 | r——上底半徑 R——下底半徑 h——高 l-------母線 | S=πr^2+πR^2+(2πr+2πR)L/2=π(r^2+R^2+rL+RL) | ![立體幾何[數學]](/img/0/d5f/nBnauM3X1EjMxEjM1ATNxMjM2UTM1QDN5MjM5ADMwAjMwUzLwUzLzAzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 立體幾何[數學] 立體幾何[數學] |
| 球體 | r——半徑 | S=4πr² | ![立體幾何[數學]](/img/1/618/nBnauM3X0UDN2UzM1MDMzYjM1UTM1QDN5MjM5ADMwAjMwUzLzAzLyYzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 立體幾何[數學] 立體幾何[數學] |
| 球缺 | h——球缺高 r——球半徑 a——球缺底半徑 a^2=h(2r-h) | | V=πh(3a^2+h^2)/6 =πh2(3r-h)/3 |
| 球檯 | r1和r2——球檯上、下底半徑 h——高 | | V=πh[3(r1ˆ2+r2ˆ2)+hˆ2]/6 |
| 圓環體 | R——環體半徑 D——環體直徑 r——環體截面半徑 d——環體截面直徑 | | V=2π^2Rr^2 =π^2Dd^2/4 |
| 桶狀體 | D——桶腹直徑 d——桶底直徑 h——桶高 | | V=πh(2D^2+d2^)/12 (母線是圓弧形,圓心是桶的中心) V=πh(2D^2+Dd+3d^2/4)/15 (母線是拋物線形) |
註:初學者會認為立體幾何很難,但只要打好基礎,立體幾何將會變得很容易。學好立體幾何最關鍵的就是建立起立體模型,把立體轉換為平面,運用平面知識來解決問題,立體幾何在高考中肯定會出現一道大題,所以學好立體是非常關鍵的。
三垂線定理
在平面內的一條直線,如果和穿過這個平面的一條斜線在這個平面內的射影垂直,那么它也和這條斜線垂直。
三垂線定理的逆定理:在平面內的一條直線,如果和穿過這個平面的一條斜線垂直,那么它也和這條斜線在平面的射影垂直。
1、三垂線定理描述的是PO(斜線),AO(射影),a(直線)之間的垂直關係。
2、a與PO可以相交,也可以異面。
3、三垂線定理的實質是平面的一條斜線和平面內的一條直線垂直的判定定理。
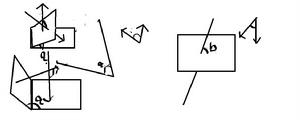
關於三垂線定理的套用,關鍵是找出平面(基準面)的垂線。至於射影則是由垂足,斜足來確定的,因而是第二位的。從三垂線定理的證明得到證明a⊥b的一個程式:一垂,二射,三證。即
 幾何模型
幾何模型 第一,找平面(基準面)及平面垂線;
第二,找射影線,這時a,b便成平面上的一條直線與一條斜線;
第三,證明射影線與直線a垂直,從而得出a與b垂直。
註:
1.定理中四條線均針對同一平面而言;
2.套用定理關鍵是找"基準面"這個參照系。
用向量證明三垂線定理。
1.已知:PO,PA分別是平面a的垂線,斜線,OA是PA在a內的射影,b屬於a,且b垂直OA,求證:b垂直PA
證明:因為PO垂直a,所以PO垂直b,又因為OA垂直b 向量PA=(向量PO+向量OA)
所以向量PA乘以b=(向量PO+向量OA)乘以b=(向量PO 乘以 b) 加 (向量OA 乘以 b )=O,
所以PA垂直b。
2.已知:PO,PA分別是平面a的垂線,斜線,OA是PA在a內的射影,b屬於a,且b垂直PA,求證:b垂直OA
證明:因為PO垂直a,所以PO垂直b,又因為PA垂直b, 向量OA=(向量PA-向量PO)
所以向量OA乘以b==(向量PA-向量PO)乘以b=(向量PA 乘以 b )減 (向量PO 乘以 b )=0,
所以OA垂直b。
3.已知三個平面OAB,OBC,OAC相交於一點O,角AOB=角BOC=角COA=60度,求交線OA於平面OBC所成的角。
向量OA=(向量OB+向量AB),O是內心,又因為AB=BC=CA,所以OA於平面OBC所成的角是30度。
二面角
定義
平面內的一條直線把平面分為兩部分,其中的每一部分都叫做半平面,從一條直線出發的兩個半平面所組成的圖形,叫做二面角。(這條直線叫做二面角的棱,每個半平面叫做二面角的面)
平面角
以二面角的棱上任意一點為端點,在兩個面內分別作垂直於棱的兩條射線,這兩條射線所成的角叫做二面角的平面角。
平面角是直角的二面角叫做直二面角。
兩個平面垂直的定義:兩個平面相交,如果它們所成的二面角是直二面角,就說這兩個平面互相垂直。
大小範圍
範圍為:0≤θ≤π;
相交時 0a=kb
m⊥n->ab=0 | | 直線-平面 | m//e->ac=0 | m⊥e->a=kc |
| 平面-平面 | e//f->c=kd | e⊥f->cd=0 |
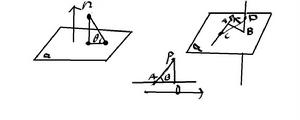
空間的角
 各種角
各種角 直線所成的角:設直線m、n的方向向量為a、b,m,n所成的角為 a。
cosa=cos =a*b/|a||b|
直線和平面所成的角:設直線m的方向向量為a,平面e的法向量為c。
設b為m和e所成的角,則b=π/2± ,sinb=|cos |=|a*c|/|a||c|
距離求解
異面直線的距離:l1、l2為異面直線,l1,l2公垂直線的方向向量為n,C、D為l1、l2上任意一點,l1到l2的距離為|AB|=|CD*n|/|n|
 距離
距離 點到平面的距離:設PA為平面的一條斜線,O是P點在a內的射影, PA和a所成的角為b,n為a的法向量。
易得:|PO|=|PA|sinb=|PA|*|cos |=|PA|*(|PA*n|/|PA||n|)=|PA*n|/|PA|
直線到平面的距離為在直線上一點到平面的距離;
平面到平面的距離為在平面上一點到平面的距離;
點到直線的距離:A∈l,O是P點在l上的射影,PA和l所成的角為b,s為l的方向向量。易得:
|PO|=|PA|*|sinb|=|PA|*|sin |=|(PA|^2|s|^2|-|PA*s|^2)^1/2/|s|
線面方程
定義
平面:在空間中,到兩點距離相等的點的軌跡叫做平面。
直線:同時屬於兩個平面的點的軌跡。
或:在平面里,到兩個點距離相等的點。
方程
平面:根據定義,設動點為M(x,y,z),兩點分別為(a,b,c)和(d,e,f)
則[(x-a)^2+(y-b)^2+(z-c)^2]^1/2
=[(x-d)^2+(y-e)^2+(z-f)^2]^1/2x^2-2ax+y^2-2by+z^2-2cz(a^2+b^2+c^2)
=x^2-2dx+y^2-2ey+z^2-2fz+(d^2+e^2+f^2)(2d-2a)x+(2e-2b)y+(2f-2c)z+(a^2-d^2+b^2-e^2+c^2-f^2)
=0
形式為ax+by+cz+d=0。
直線:根據定義,可列方程組:
ax+by+cz+d=0
ex+fy+gz+h=0
得其形式是:
x=jz+k
y=lz+m
線面求法
(1)三點式
則三點同時滿足
ax0+by0+cz0+d=0
ax1+by1+cz1+d=0
ax2+by2+cz2+d=0
可得出a-b-c-d的關係,再把d取特殊值,解方程。
(2)點線式
可線上上找兩個點,轉化成三點式。
(3)雙線式(不異面)
可在兩個線上共找三個點,轉化成三點式。得:ax+by+cz+d=0
(4)線斜式
斜率:該平面和xOy平面的二面角的正切。
求法:設該平面為ax+by+cz+d=0,xOy是z=0
即k=c/(a^2+b^2+c^2)且它通過y=kx+b,z=lz+a
根據判定,可得a-b-c-d的關係。再把d賦特殊值。
(5)兩點式
用待定係數法求出k,l,m,n的關係,再取特殊值。
向量求法
直線:截取直線l上兩點A(l,n,0)和B(k+l,m+n,1)方向向量為:AB=(k,m,1)
平面:取平面內三點:A(0,0,-d/c)B(1,1,-(d+b+a)/c)C(0,2,-(d+2b)/c)
AC=(0,2,-2b/c)AB=(1,1,-(a+b)/c)
設向量n:(x,y,c)為平面的法向量,則
2y-2b=0 x+y-(a+b)=0
y=b x=a
則n=(a,b,c)為平面的一個法向量。
直線平面的關係
直線和直線:
設設直線方程為x=k1z+l1,y=m1z+n1和x=k2z+l2,y=m2z+n2
相交:兩條直線所組成的方程組有實數解
平行:k1/k2=m1/m2且l1/l2≠n1/n2
異面:不相交也不平行
垂直:k1k2+m1m2=-1
直線和平面
設直線方程為x=kz+b,y=lz+a,平面方程為cx+dy+ez+f=0,p=k+l+e,q=a+b+f
屬於:p=0,q=0
平行:p=0,q≠0
相交:p≠0
垂直:k/c=b/d=e
平面和平面
設平面方程為ax+by+cz+d=0和ex+fy+gz+h=0,p=a/e,q=b/f,r=c/g,s=d/h
相交:不平行
平行:p=q=r≠s
垂直:ae+bf+cg=0
知識點總結
1.直線在平面內的判定
(1)利用公理1:一直線上不重合的兩點在平面內,則這條直線在平面內。
(2)若兩個平面互相垂直,則經過第一個平面內的一點垂直於第二個平面的直線在第一個平面內,即若α⊥β,A∈α,AB⊥β,則AB∈α。
(3)過一點和一條已知直線垂直的所有直線,都在過此點而垂直於已知直線的平面內,即若A∈a,a⊥b,A∈α,b⊥α,則a∈α。
(4)過平面外一點和該平面平行的直線,都在過此點而與該平面平行的平面內,即若P∈α,P∈β,β不平行α,P∈a,a∥α,則a∈β。
(5)如果一條直線與一個平面平行,那么過這個平面內一點與這條直線平行的直線必在這個平面內,即若a包含於α,A∈α,A∈b,b∥a,則b包含於α。
2.存在性和唯一性定理
(1)過直線外一點與這條直線平行的直線有且只有一條;
(2)過一點與已知平面垂直的直線有且只有一條;
(3)過平面外一點與這個平面平行的平面有且只有一個;
(4)與兩條異面直線都垂直相交的直線有且只有一條;
(5)過一點與已知直線垂直的平面有且只有一個;
(6)過平面的一條斜線且與該平面垂直的平面有且只有一個;
(7)過兩條異面直線中的一條而與另一條平行的平面有且只有一個;
(8)過兩條互相垂直的異面直線中的一條而與另一條垂直的平面有且只有一個。
3.射影及有關性質
(1)點在平面上的射影:自一點向平面引垂線,垂足叫做這點在這個平面上的射影,點的射影還是點。
(2)直線在平面上的射影:自直線上的兩個點向平面引垂線,過兩垂足的直線叫做直線在這平面上的射影,和射影面垂直的直線的射影是一個點;不與射影面垂直的直線的射影是一條直線。
(3)圖形在平面上的射影:一個平面圖形上所有的點在一個平面上的射影的集合叫做這個平面圖形在該平面上的射影。當圖形所在平面與射影面垂直時,射影是一條線段;當圖形所在平面不與射影面垂直時,射影仍是一個圖形。
(4)射影的有關性質:從平面外一點向這個平面所引的垂線段和斜線段中:(i)射影相等的兩條斜線段相等,射影較長的斜線段也較長;(ii)相等的斜線段的射影相等,較長的斜線段的射影也較長;(iii)垂線段比任何一條斜線段都短。
4.空間中的各種角等角定理及其推論定理
若一個角的兩邊和另一個角的兩邊分別平行,並且方向相同,則這兩個角相等.推論若兩條相交直線和另兩條相交直線分別平行,則這兩組直線所成的銳角(或直角)相等。異面直線所成的角
(1)定義:a、b是兩條異面直線,經過空間任意一點O,分別引直線a′a,b′∥b,則a′和b′所成的銳角(或直角)叫做異面直線a和b所成的角。
(2)取值範圍:0°
(3)求解方法:根據定義,通過平移,找到異面直線所成的角θ;解含有θ的三角形,求出角θ的大小。
5.直線和平面所成的角
(1)定義:和平面所成的角有三種:(i)垂線 面所成的角的一條斜線和它在平面上的射影所成的銳角,叫做這條直線和這個平面所成的角。(ii)垂線與平面所成的角 直線垂直於平面,則它們所成的角是直角。(iii)一條直線和平面平行,或在平面內,則它們所成的角是0°的角。
(2)取值範圍:0°≤θ≤90°
(3)求解方法:作出斜線在平面上的射影,找到斜線與平面所成的角θ.解含θ的三角形,求出其大小.最小角定理斜線和平面所成的角,是這條斜線和平面內經過斜足的直線所成的一切角中最小的角,亦可說,斜線和平面所成的角不大於斜線與平面內任何直線所成的角。
6.二面角及二面角的平面角
(1)半平面: 直線把平面分成兩個部分,每一部分都叫做半平面。
(2)二面角: 條直線出發的兩個半平面所組成的圖形叫做二面角。這條直線叫做二面角的棱,這兩個平面叫做二面角的面,即二面角由半平面一棱一半平面組成.若兩個平面相交,則以兩個平面的交線為棱形成四個二面角。二面角的大小用它的平面角來度量,通常認為二面角的平面角θ的取值範圍是0°
(3)二面角的平面角:以二面角棱上任意一點為端點,分別在兩個面內作垂直於棱的射線,這兩條射線所組成的角叫做二面角的平面角。二面角的平面角具有下列性質:(i)二面角的棱垂直於它的平面角所在的平面,即AB平面PCD。(ii)從二面角的平面角的一邊上任意一點(異於角的頂點)作另一面的垂線,垂足必在平面角的另一邊(或其反向延長線)上。(iii)二面角的平面角所在的平面與二面角的兩個面都垂直,即平面PCDα,平面PCDβ。③找(或作)二面角的平面角的主要方法:(i)定義法。(ii)垂面法。(iii)三垂線法。(iiii)根據特殊圖形的性質。
(4)求二面角大小的常見方法:先找(或作)出二面角的平面角θ,再通過解三角形求得θ的值。利用面積射影定理S′=S·cosα其中S為二面角一個面內平面圖形的面積,S′是這個平面圖形在另一個面上的射影圖形的面積,α為二面角的大小。利用異面直線上兩點間的距離公式求二面角的大小。
7.空間的各種距離點到平面的距離
(1)定義: 面外一點引一個平面的垂線,這個點和垂足間的距離叫做這個點到這個平面的距離.
(2)求點面距離常用的方法:
1)直接利用定義求找到(或作出)表示距離的線段;抓住線段(所求距離)所在三角形解之。
2)利用兩平面互相垂直的性質.即如果已知點在已知平面的垂面上,則已知點到兩平面交線的距離就是所求的點面距離。
3)體積法其步驟是:在平面內選取適當三點,和已知點構成三稜錐;求出此三稜錐的體積V和所取三點構成三角形的面積S;由V=S·h,求出h即為所求。這種方法的優點是不必作出垂線即可求點面距離。難點在於如何構造合適的三稜錐以便於計算。
4)轉化法將點到平面的距離轉化為(平行)直線與平面的距離來求。
8.直線和平面的距離
(1)定義:一條直線和一個平面平行,這條直線上任意一點到平面的距離,叫做這條直線和平面的距離.
(2)求線面距離常用的方法:直接利用定義求證(或連或作)某線段為距離,然後通過解三角形計算之。將線面距離轉化為點面距離,然後運用解三角形或體積法求解之。作輔助垂直平面,把求線面距離轉化為求點線距離。
9.平行平面的距離
(1)定義:兩個平行平面同時垂直的直線,叫做這兩個平行平面的公垂線。公垂線夾在兩個平行平面間的部分,叫做這兩個平行平面的公垂線段。兩個平行平面的公垂線段的長度叫做這兩個平行平面的距離。
(2)求平行平面距離常用的方法:直接利用定義求證(或連或作)某線段為距離,然後通過解三角形計算之。把面面平行距離轉化為線面平行距離,再轉化為線線平行距離,最後轉化為點線(面)距離,通過解三角形或體積法求解之。
10.異面直線的距離
(1)定義:與異面直線都垂直相交的直線叫做兩條異面直線的公垂線。兩條異面直線的公垂線在這兩條異面直線間的線段的長度,叫做兩條異面直線的距離。任何兩條確定的異面直線都存在唯一的公垂線段。
(2)求兩條異面直線的距離常用的方法:(1)定義法題目所給的條件,找出(或作出)兩條異面直線的公垂線段,再根據有關定理、性質求出公垂線段的長。此法一般多用於兩異面直線互相垂直的情形。(2)轉化法:為以下兩種形式:線面距離面面距離③等體積法④最值法⑤射影法⑥公式法。
定理口訣
點線面三位一體,柱錐檯球為代表。距離都從點出發,角度皆為線線成。
垂直平行是重點,證明須弄清概念。線線線面和面面、三對之間循環現。
方程思想整體求,化歸意識動割補。計算之前須證明,畫好移出的圖形。
立體幾何輔助線,常用垂線和平面。射影概念很重要,對於解題最關鍵。
異面直線二面角,體積射影公式活。公理性質三垂線,解決問題一大片。
 各種各樣的幾何立體圖形
各種各樣的幾何立體圖形 ![立體幾何[數學]](/img/f/d66/nBnauM3X3gjM3MDOyITM0MjM2UTM1QDN5MjM5ADMwAjMwUzLyEzL0QzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 立體幾何[數學]
立體幾何[數學] ![立體幾何[數學]](/img/4/cb5/nBnauM3XwEjNwYjMxgDNxMDN0UTMyITNykTO0EDMwAjMwUzL4QzLzAzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 立體幾何[數學]
立體幾何[數學] ![立體幾何[數學]](/img/1/72b/nBnauM3X2cjN4cTM1IzM0IDN0UTMyITNykTO0EDMwAjMwUzLyMzL2gzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 立體幾何[數學]
立體幾何[數學] ![立體幾何[數學]](/img/0/d5f/nBnauM3X1EjMxEjM1ATNxMjM2UTM1QDN5MjM5ADMwAjMwUzLwUzLzAzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 立體幾何[數學]
立體幾何[數學] ![立體幾何[數學]](/img/1/618/nBnauM3X0UDN2UzM1MDMzYjM1UTM1QDN5MjM5ADMwAjMwUzLzAzLyYzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 立體幾何[數學]
立體幾何[數學]  幾何模型
幾何模型  各種角
各種角  距離
距離 