氣體的黏性
 空氣黏度
空氣黏度粘性是真實流體的一個重要輸運性質,定義為流體在經受切向(剪下)力時發生形變以反抗外加剪下力的能力,這種反抗能力只在運動流體相鄰流層間存在相對運動時才表現出來。為了理解這一概念,我們用一個能突出表現空氣粘性的實例來說明。如圖1-1所示,將一個無限薄的平板放置在風洞中,板面平行於氣流方向,圖中給出了用風速儀測量的平板附近沿法線方向上的氣流速度分布。可以看出,在板面上氣流速度為零,越向外速度越大,且直到離開板面一定距離δ處,速度才與來流速度沒有顯著差別。平板附近的這種速度分布正是空氣的粘性造成的,粘性使平板上的流體層完全貼附在靜止的板面上,這種與板面完全沒有相對速度的情況稱為無滑移條件(no-slip condition)。稍外的一層空氣受到氣體層與氣體層之間的摩擦作用,被板面上的那層靜止空氣所牽制,其速度也是下降到了接近於零,但由於它已離開板面一個極小的距離,速度比零要稍大些。粘性的牽製作用就這樣一層一層的向外傳遞,因此,離開板面越遠,氣流速度越大。從速度的梯度變化來說,越靠近平板板面,速度梯度越大,隨著離開板面距離的增加速度梯度逐漸減小。
從分子運動論的觀點看,可以認為粘性是由於具有不同速度的相鄰流體層之間的分子交換而產生的動量遷移的結果,是分子熱運動引起的動量輸運。
定義
空氣黏度,又稱空氣動力黏度,舊稱黏性係數。表征空氣黏性的一個物理量。是分子自由層碰撞抵制剪下變形的能力。
 空氣黏度
空氣黏度牛頓經過長期的試驗研究,於1686年確定了流體黏性內摩擦定律,指出不同流速的流體層間的摩擦力的大小與流體的動力黏性係數有直接的關係,即:
 空氣黏度
空氣黏度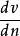 空氣黏度
空氣黏度 空氣黏度
空氣黏度其中是速度梯度,是單位面積上的摩擦力。
該定義式指出了動力黏性係數的物理意義:當流體的運動速度梯度為1時,層間單位面積上的黏性摩擦力:就是動力粘性係數。因為它包含了動力學單位,所以也被成為動力粘性係數。動力粘性係數是流體的一種屬性,表征流體粘性的大小。動力粘性係數的大小與流體的種類和溫度關係密切。流體種類不同則粘性不同;同一種流體的粘性隨溫度的不同也有很人的差別一般地,液體的粘性隨溫度升高而降低,氣體的粘性隨溫度升高而增加。
當流體確定為空氣時,則表現為空氣動力粘度,上述公式依然適用。
運動黏性係數
工程計算中經常要涉及到黏性的概念,流體的粘性大小一般用黏性係數來衡量。黏性係數通常有動力黏性係數和運動黏性係數之分,無論從概念上和意義上兩者都有著本質的區別,對不同流體之間粘性的大小進行比較時,只能使用動力粘性係數的數值,不應當因為兩者都稱為“粘性係數”而任意選用,否則可能會造成錯誤的結論在一些文章甚至教科書中有時會見到將兩者混淆、隨意引用進行流體進行粘性大小比較的情況。
工程計算中還會經常引用另一粘性係數—運動粘性係數。運動粘性係數與動力粘性係數絕然不同,它沒有任何物理意義,只是人為地將其定義為動力粘性係數與流體密度的比值。
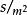 空氣黏度
空氣黏度在國際單位制中其單位為 ,因為包含了運動學單位,所以被稱為運動粘性係數運動粘性係數只能用來比較同一種流體在不同溫度下粘性的相對大小,它不代表粘性的絕對值,更不能用它進行不同種類流體間粘性大小的比較,尤其是對密度相差較大的不同流體,否則就會得出相反的結論。
動力粘性係數還因為它代表了兩個物理參數的比值,可以簡化很多含有該比值的計算公式。關於流體的技術手冊中一般都可查到運動粘性係數的數值,使工程計算得以簡化。

