種群動態模型
單種種群模型
種群在無限環境中的指數增長模型 自然種群是在現實的有限的環境中增長的。這裡先介紹一個理想種群在無限環境中的增長模型。種群增長可分為離散增長和連續增長兩類。
如果現實種群只由一個世代構成,相繼世代之間沒有重疊,種群增長就屬於離散型。例如棲息於草原季節性小水坑中的水生昆蟲,每年雌蟲產一次卵,卵孵化長成幼蟲,蛹在泥中渡過旱季,到第二年才變為成蟲,世代不相重疊。相反,世代之間有重疊,種群就接近連續增長型。
世代不相重疊種群的離散增長型(差分方程) 假定從一個繁殖季節t0開始,有N0個雌體和同等量的雄體(這樣就能簡單地以雌體產生雌體來代表種群增長),其產卵量為B,總死亡為D,那么到下一年,t1時,其種群數量N1為(假定種群沒有遷入和遷出):
N1=N0+B-D。
以λ代表種群兩個世代的比率:λ=N1/N0;如果種群在無限環境中年復一年地以這個速率增長,則
N1=N0λ
N2=N1λ
N3=N2λ
.........
Nt+1=Ntλ
或Nt=N0λt。
λ在此稱為周限增長率。這種種群增長形式稱為幾何級數式增長或指數式增長。
對方程式Nt=N0λt兩邊取對數值,則
lgNt=lgN0+tlgλ。
 種群動態P
種群動態P 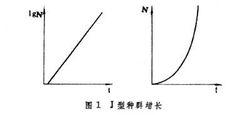 種群動態P
種群動態P 它具有直線方程y=α+bx的形式。因此,以1gNt對t作圖,就能得到一條直線,其中1gN0是直線的截距,1gλ是直線的斜率。如果我們觀察到一個種群,用其數量的對數與時間作圖,可以得到一條直線,那么就能知道,這個種群象我們的模型一樣,具有恆定的增長率,其增長率未受其他因素的限制,同時,按照直線的斜率,就能知道這個種群的周限增長率λ。
這個模型中只有一個參數λ,它是一個有用的量,如果λ=1即Nt+1/Nt=1,則種群數量在t+1時和t時相等,即種群穩定。事實上有 4種可能:λ>1,種群上升;λ=1,種群穩定;λλ=0,種群在一代中滅亡。
世代重疊種群的連續增長模型(微分方程) 如果世代之間有重疊,種群數量以近似連續的方式改變,通常就用微分方程來描述。對於在無限環境中瞬時增長率保持恆定的種群,種群增長仍表現為指數式增長過程,即其積分式為Nt=N0。
式中 e為自然對數的底;r為種群的瞬時增長率。假定b和d為種群的瞬時出生率和瞬時死亡率,那么瞬時增長率r=(b-d)(假定沒有遷入和遷出)。
例如,初始種群N0為100,r為0.5/年,則以後的種群數量(見表)。
1nNt=1nN0+rt
變形得代入1949年和1978年人口數字得1949年以來,中國人口自然增長率為0.0192或19.2‰,即平均每年每1000人增加19.2人。轉成周限增長率,λ=er=e0.0192=1.0193,即每年為前一年的1.02倍。
用指數增長模型還可以進行預測。人口預測中常用人口加倍時間td,所謂人口加倍,即Nt/N0=2,因此,
2=
1n 2=rtd
td=1n 2/r
 種群動態P
種群動態P 把r=0.0192代入td=0.6913/0.0192≈35年。這就是說,如果中國人口還按1949年以後的平均速度增長,大約35年就要翻一番。
指數增長是無界的,自然種群不可能長期按幾何級數增長。一對蒼蠅或一個細菌,若按此模型增長,不須很久就將占有地球表面全部空間。因此指數增長只能在短期內、當空間和各種資源對種群數量相對地沒有任何限制的情況下才能表現出來。有學者稱r為種群的內稟增長能力也稱馬爾薩斯參數rm(因為此模型由T.R.馬爾薩斯於1798年提出)。指數式增長的不現實性,使學者提出了邏輯斯諦增長模型。
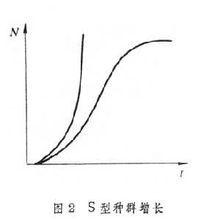
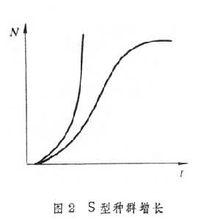
種群在有限環境下的邏輯斯諦增長模型 假定種群增長有一個環境所允許的最大種群值,稱為容納量,通常以K表示。當種群大小達到K時,種群不再增長,即dN/dt=0。另假定隨著種群密度上升,種群增長率的降低是逐漸的、按比例的,即每增加一個個體的影響是1/K。根據這兩個假定,種群增長曲線呈S型(圖2),邏輯斯諦方程可以很好地描述這種S型增長。式中r為種群潛在增長率;K為種群數量的最大值,即環境的容納量。是種群增長率隨密度增加而按比例減少的修正項,據此:當N接近於零時,接近於1,r能充分實現;當N=K時,等於零,r完全不能實現,種群停止增長;當N由0→K時,項由1→0,r能實現的程度逐漸降低。由此,邏輯斯諦方程可用語言表達為:種群增長率等於種群潛在的最大增長率與最大增長的實現程度的乘積。
對草履蟲、果蠅、擬谷盜、米象的實驗種群研究,都證明其種群增長呈 S型邏輯斯諦增長。某些動物的自然種群增長,如環頸雉引入華盛頓州、綿羊引入澳大利亞以後,也表現了初期的邏輯斯諦增長。R.珀爾甚至將邏輯斯諦增長認為是種群增長的普遍規律。海洋漁業資源利用中的最大持續產量原理的一個重要理論基礎,就是種群的邏輯斯諦增長理論。
邏輯斯諦曲線在N=K/2處有一個拐點,在拐點處dN/dt最大。在到達拐點前,dN/dt的值隨種群增加而上升,為正加速期,拐點後則為負加速期。由此可見,邏輯斯諦方程描述了這樣一種機制:種群有按指數式增長的潛在能力,但當密度上升時,種群能實現的有效增長率逐漸降低。就是說,在種群增長率與種群自身密度之間存在著反饋機制,種群密度越高,這種對種群增長率的負影響也越大。顯然,這是一種密度制約作用。
邏輯斯諦方程的一個主要缺陷是種群穩定在K值,這一點是不符合實際的。自然種群處於經常的變動之中;其中有不規則變動,也有周期性變動,說它一定穩定在K值這是缺乏證據的。其次,邏輯斯諦模型本身包含著這樣的假定:密度增加對種群增長率的負影響作用是立即發生的,沒有任何時滯,而多數自然種群難以符合這個假定。例如對某些昆蟲來說,高密度對出生率的影響要延遲到成蟲種群減少時才表現出來,這大約要經過一個世代;又如以節制生育來控制人口,由於時滯,真正看到效果(即人口下降)要在幾十年之後。
兩種種群相互作用模型
競爭模型 這裡指的競爭是兩個具有共同食物、空間或其他需求的物種之間的競爭,不包括捕食、寄生關係等廣義的生存競爭。G.F.高斯以兩種分類上和生態上很接近的草履蟲(即雙小核草履蟲和大草履蟲)進行試驗。在對兩種草履蟲分別培養時,它們都表現出典型的“S”型增長曲線,但在混合培養時,開始兩種都有增長,最後大草履蟲滅亡,雙核小草履蟲生存。高斯用A.J.洛特卡-V.沃爾泰拉模型擬合這些結果,並在此基礎上提出競爭排除原理,即兩個生態要求完全相似的物種不可能共存的原理。洛特卡-沃爾泰拉競爭模型以邏輯斯諦增長為基礎。假定物種甲、乙單獨增長時,均按邏輯斯諦方程,即:對物種甲,對物種乙, 邏輯斯諦增長方程說明種群的增長率 dN/dt決定於種群已積聚的密度N、內稟增長能力r和種群增長尚未利用的“資源”。當兩個物種在同一環境中增長時,每一物種的增長率也決定於這 3項,但最後一項比單種種群複雜。物種甲的環境容納量K1,除被本物種N1利用以外,還被混群增長中另一物種N2同時利用。同樣的環境資源,對不同種動物的最大容納量在大多數情況下是不同的,一個N1個體所占的資源不會與一個N2個體所占的相同。但可以找出一個係數來表示每一個N2個體所占資源與每個N1個體所占資源的比例,即:αN2=N1。式中α為物種乙對物種甲的競爭係數。如果α等於1,說明一個N2個體所占用資源與一個N1個體所占用的相等;如果αN2個體所占用資源多於一個N1個體所占用的;如果α>1,則表示一個N2個體所占用資源不足一個N1個體所占用的。
假定α是一個常數,即在所有各種密度配合下,兩種競爭者的競爭係數不變,這樣,物種甲在混種種群中的競爭方程是:這個方程中與單種邏輯斯諦增長方程相比,只在“剩餘資源”(未利用資源)項中,增加了一個αN2,表示K1資源除為物種甲(N1)所占用以外,同時還為物種乙(αN2)所占用。
同樣,對於物種乙而言,物種甲的競爭係數 β可根據N2=βN1而估計,物種乙的競爭方程是:這就是A.J.洛特卡和V.沃爾泰拉在1925年和1926年分別獨立提出的著名的競爭方程。
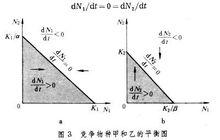
從理論上講,兩個物種在一起競爭時,可能產生的結局有 3種:①物種甲被擠掉,僅物種乙生存下來;②僅物種甲生存下來;③物種甲和乙共存。若物種甲對物種乙的抑制性效應較強,則物種甲將取勝,反之則物種乙取勝。這種直覺的結局可通過數學方法來估計(圖3):
dN1/dt=0=dN2/dt
 種群動態P
種群動態P 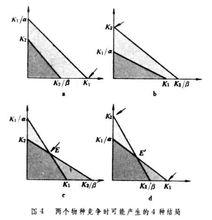 種群動態P
種群動態P 把圖3的a和b互相疊合起來,就可以得到4種不同的結局(圖4)。圖4中水平的影線區表示物種甲將增長,而垂直的影區表示物種乙將增長。這 4種情況決定於K1、K2、K1/α和K2/β 等4個值的大小。圖 4a表示物種甲取勝,物種乙被排擠掉。這種情況發生在K1>K2/β,K2K1/α的時候。圖4b表示物種乙取勝,物種甲被排擠掉。情況正好與a相反,即發生在K2>K1/α,K1K2/β 的時候。圖4c表示兩個物種共存,並形成穩定平衡的局面。這種情況產生在K1K2/β 和K2K1/α的時候,兩條對角線相交,其交點就是平衡點。由於K1K2/β,在三角形K1EK2/β 中,物種甲不能增長,而乙能增長,箭頭向平衡點收斂。同樣,因為K2K1/α,在三角形K1/αEK2中物種乙不能增長,而甲能增長,箭頭也向平衡點收斂,從而形成穩定的平衡。圖4d中當K1>K2/β,K2>K1/α時,兩條對角線相交,也出現平衡點,但這種平衡是不穩定的。因為K1>K2/β,在三角形K1EK2/β中,物種乙不能增長,物種甲能增長,箭頭不收斂,物種甲將取勝。同樣,因為K2>K1/α,在三角形K2EK1/α中,物種甲不能增長,物種乙能增長,箭頭也不收斂,物種乙將取勝。因此,平衡是不穩定的,甲乙兩個物種都有可能取勝,其結局將取決於競爭開始時,哪一物種在數量上占優勢。 根據上面分析,競爭的結局決定於α、β、K1和K24 個值的大小。因為α與 β是兩物種彼此之間的競爭係數,所以α/K1是物種乙對於物種甲的種間競爭強度指標,β /K2是物種甲對於物種乙的種間競爭強度指標。 另一方面,1/K1可以作為物種甲的種內競爭強度指標,而1/K2是物種乙的種內競爭強度指標。由此可見,競爭的結局取決於種內競爭和種間競爭的相對大小。如果某物種的種內競爭大,種間競爭力小,該物種將失敗;反之,某物種種內競爭小,而種間競爭力大,該物種取勝。
洛特卡-沃爾泰拉競爭模型對於預測兩個競爭物種互動作用的結果很有用,但是正像單種種群的增長模型一樣,其有效度取決於建立模型的假定是否符合實際。在此模型中,不但假定了K1、K2、r1、r2是常數,而且還假定競爭係數α和 β是常數。競爭係數是一個複雜的因素,它受自然選擇的影響並隨時間和種群密度而變化。另外,兩個物種的空間分布和年齡結構也將影響競爭係數。儘管如此,這個簡單模型仍有助於理解一個種群的數量如何影響另一個種群的數量和預測競爭的各種結局。
洛特卡-沃爾泰拉的競爭方程還可以擴充套用於多個物種的競爭: J.H.范德梅爾(1969)曾以4種草履蟲混合培養,結果與上一方程組預測值進行比較,擬合良好。
捕食模型 經典的捕食者-獵物模型也是由洛特卡和沃爾泰拉提出的。
洛特卡-沃爾泰拉的捕食模型:假定在沒有捕食者的條件下,獵物種群按幾何級數增長,即dN/dt=r1N;對於捕食者,假定在沒有獵物條件下,種群按幾何級數減少,即dP/dt=-r2P;假如捕食者和獵物種群處在相互作用中,獵物種群的增長率將因捕食作用而降低,降低程度隨捕食者數量而變。因此:
dN/dt=(r1-εP)N
式中ε在此是測度捕食壓力的常數,即平均每一捕食者殺死獵物的常數。可以構想,如果ε=0,那么-εP一項等於零,獵物就完全逃脫了捕食者的捕食。ε越大,表示捕食者對獵物的壓力也越大。同樣,捕食者種群的增長率也將依賴於獵物的密度:
dP/dt=(-r2+θN)P
 種群動態P
種群動態P 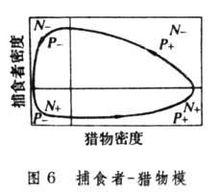 種群動態P
種群動態P 式中θ是測度捕食者因捕食獵物而產生出更多捕食者的常數。這個值越大,捕食效率越高,捕食者種群增長的效應也越大。
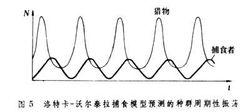
洛特卡-沃爾泰拉的捕食模型的解答具有這樣的特徵:捕食者和獵物種群產生周期性振盪,而振幅決定於兩者的初始密度,以(圖5)為例,r1=1.0,ε=0.1,r2=0.5,θ=0.02,而初始條件是N0=20,P0=4。如果將圖5的結果以捕食者密度為縱坐標、獵物密度為橫座標、按時間順序作出相點陣圖,就可以得到一個封閉環(圖6)。相點陣圖表示兩個種群的密度將按封閉環的軌道逆時針方向無限循環,其中心點即為平衡點(N=r2/θ=0.5/0.02=25,P=r1/ε=1.0/0.1=10),通過平衡點作互相垂直的線,將相點陣圖分為4塊,在垂直線右面捕食者種群增加,在左面減少,在水平線下面,獵物種群增加,在上面減少。因此,洛特卡-沃爾泰拉模型表明獵物-捕食者種群動態中分4個時期:①獵物增加,捕食者也增加;②獵物減少,捕食者繼續增加;③獵物和捕食者都減少;④捕食者繼續減少,而獵物增加。如此循環不息。
G.F.高斯為檢驗此模型曾做過著名的試驗。他以雙環櫛毛蟲作為捕食者,大草履蟲作為獵物,在定期更新的小麥浸出液中培養。
高斯的試驗分3期:第1期以均勻的液體介質作培養環境,其結果總是草履蟲種群首先增長,隨後櫛毛蟲種群上升,然後雙環櫛毛蟲將草履蟲捕食殆盡,隨之櫛毛蟲也因飢餓而死亡。試驗結果並未出現洛特卡-沃爾泰拉模型所預測的那種捕食者-獵物系統的周期性波動。但是高斯相信,試驗之所以未獲得理論上預期的周期性振盪,是由於櫛毛蟲增殖過快。在第2期試驗中,高斯考慮一個較複雜的系統,他在培養管的底部放進一些沉渣,使草履蟲能隱蔽起來,結果是櫛毛蟲消滅了液相中草履蟲,然後由於飢餓而死亡,但隱蔽在沉渣中的草履蟲增殖,於是以獵物種群增長而捕食者死亡而結束,結果又未證實洛特卡-沃爾泰拉模型所預測的周期性波動。在第3期試驗中,高斯定期地(每3天)加入一個草履蟲和一個櫛毛蟲(模擬遷入),結果得到了獵物-捕食者種群的周期性振盪。