在電化學中,Cottrell方程描述了在受控電位實驗中電流相對於時間的變化,例如計時電流法。 具體來說,它描述當電位是階梯函式時的電流回響。 它由1903年的弗雷德里克·加德納·科特雷爾(Frederick Gardner Cottrell)提出。對於簡單的氧化還原事件,如二茂鐵/二茂鐵鹽的組合,測得的電流取決於分析物擴散到電極的速率。 也就是說,電流被稱為“擴散控制”。 Cottrell方程描述了平面的電極的情況,但也可以通過使用相應的拉普拉斯運算元和邊界條件結合Fick的第二擴散定律來推衍球形,圓柱形和矩形幾何形狀。
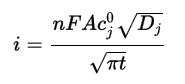 科特雷爾方程
科特雷爾方程i =電流,單位A
n =電子數(例如為了減少/氧化一分子的分析物j)
F =法拉第常數,96,485C / mol
A =(平面)電極的面積(cm2)
cj0 =可還原分析物j的初始濃度,單位為mol / cm3;
Dj =物種j的擴散係數,單位為cm 2 / s
t =時間 單位s。
i對t-1/2圖中與線性的偏離有時表明氧化還原事件與其他過程相關,例如配體的締合,配體的解離或幾何變化。
在實踐中,Cottrell方程簡化為i = kt-1/2,其中k是給定系統(n,F,A,cj0,Dj)的常數集合。
