基本定義
直方脈衝的波形在時域內比較尖銳,因而在頻域內占用的頻寬是無限的。如果讓這個脈衝經過一個低通濾波器,即讓它的頻率變窄,那么它在時域內就一定會變寬。因為脈衝是一個序列,這樣相鄰的脈衝間就會相互干擾。這種現象被稱為碼間串擾(InterSymbol Interference,ISI)。信道總是帶限的,帶限信道對通過的的脈衝波形進行拓展。當信道頻寬遠大於脈衝頻寬時,脈衝的拓展很小,當信道頻寬接近於信號的頻寬時,拓展將會超過一個碼元周期,造成信號脈衝的重疊,稱為碼間串擾。
碼間干擾是數字通信系統中除噪聲干擾之外最主要的干擾,它與加性的噪聲干擾不同,是一種乘性的干擾。造成碼間干擾的原因有很多,實際上,只要傳輸信道的頻帶是有限的,就會造成一定的碼間干擾。
消除碼間串擾的基本思想
由於數字信息序列是隨機的,要想通過在接收濾波器輸出的信號抽樣信號中的各項相互抵消使碼間串擾為0是不行的,這就需要對基帶傳輸系統的總傳輸特性h(t)的波形提出要求。如果相鄰碼元的前一個碼元的波形到達後一個碼元抽樣判決時刻已經衰減到0,就能滿足要求。但是,這樣的波形不易實現,因為現實中的h(t)波形有很長的“拖尾”,也正是由於每個碼元的“拖尾”造成了對相鄰碼元的串擾。這就是消除碼間串擾的基本思想。
無碼間串擾的條件
只要基帶傳輸系統的衝激回響波形h(t)僅在本碼元的抽樣時刻上有最大值,並在其他碼元的抽樣時刻上均為0,則可消除碼間串擾。即,若對h(t)在時刻t=kTs(這裡假設信道和接收濾波器所造成的延遲t0=0)抽樣,則應有下式成立:
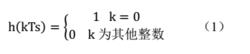 碼間串擾
碼間串擾上式(1)稱為無碼間串擾的時域條件。即,若h(t)的抽樣值除了在t=0時不為零外,在其他所有抽樣點上均為零,就不存在碼間串擾。
 碼間串擾
碼間串擾無碼間串擾的傳輸特性的設計
1.理想低通特性
滿足奈奎斯特第一準則的有很多種,一種極限情況,就是為理想低通型,即
 碼間串擾
碼間串擾當h(t)等於正負kTs(k不等於0)時有周期性零點,當傳送序列的時間間隔為Ts時,正好巧妙地利用了這些零點,只要接收端在t=kTs時間點上抽樣,就能實現無碼間串擾。
令人遺憾的是,雖然理想低通傳輸特性達到了基帶系統的極限傳輸速率和極限頻帶利用率,可是這種特性在物理上是無法實現的。而且,它的衝激回響h(t)作為傳輸波形仍然是不適宜的。
2.餘弦滾降特性
為了解決理想低通特性存在的問題,可以使理想低通濾波器特性的邊沿緩慢下降,這稱為滾降。只要H(w)在滾降段中心頻率處呈奇對稱的振幅特性,就必然可以滿足奈奎斯特第一準則,從而實現無碼間串擾傳輸。這種設計也可看成是理想特性以奈奎斯特頻寬為中心按奇對稱條件進行滾降的結果。設計的關鍵參數是滾降係數。
這種系統所占的頻頻寬,是理想低通系統的2倍。
