簡介
電子硬體隨機數發生器的主要套用是加密技術，它們用於生成隨機加密密鑰以安全地傳輸數據。它們廣泛用於Internet加密協定，如Secure Sockets Layer（SSL）。
隨機數發生器也可以通過“隨機”巨觀過程構建，使用硬幣翻轉，骰子，輪盤和彩票機等設備。不穩定動力系統理論和混沌理論可以證明這些現象存在不可預測性。儘管巨觀過程在牛頓力學下是確定性的，但是在輪盤中設計精良的設備的輸出在實踐中無法預測，因為它取決於每次使用的初始條件的敏感微觀細節。
儘管骰子主要用於賭博，並且作為遊戲中的“隨機化”元素（例如角色扮演遊戲），維多利亞時代的科學家弗朗西斯·高爾頓描述了一種使用骰子在1890年為科學目的明確生成隨機數的方法。
硬體隨機數發生器通常每秒產生有限數量的隨機比特。為了提高數據速率，它們通常用於為更快的加密安全偽隨機數生成器生成“種子”，然後生成偽隨機數輸出序列。
這樣的設備通常是基於一些能生成低等級、統計學隨機的“噪聲”信號的微觀現象，如熱力學噪聲、光電效應和量子現象。這些物理過程在理論上是完全不可預測的，並且已經得到了實驗的證實。硬體隨機數生成器通常由換能器、放大器和模擬數字轉換器組成。其中換能器用來將物理過程中的某些效果轉換為電信號，放大器及其電路用來將隨機擾動的振幅放大到巨觀級別，而模擬數字轉換器則用來將輸出變成數字，通常是二進制的零和一。通過重複採樣這些隨機的信號，一系列的隨機數得以生成。
使用
首先在賭博的背景下研究不可預測的隨機數，並且首先開發許多隨機化裝置，例如骰子，洗牌紙牌和輪盤賭輪，以用於此類用途。 相當生產的隨機數對於電子賭博至關重要，而創建它們的方式有時會受到政府博彩委員會的監管。
隨機數字也用於非賭博目的，無論是在數學上如何使用它們，例如民意調查的抽樣，以及通過隨機化近似公平性的情況，例如選擇陪審員和軍事選秀彩票。
加密
硬體隨機數生成器的主要用途是在數據加密領域，例如創建隨機加密密鑰以加密數據。 它們是偽隨機數生成器（PRNG）的更安全的替代方案，PRNG是計算機中常用於生成“隨機”數字的軟體程式。 PRNG使用確定性算法來產生數字序列。 雖然這些偽隨機序列通過隨機性的統計模式測試，但通過知道算法和用於初始化它的條件（稱為“種子”），可以預測輸出。 由於PRNG生成的數字序列是可預測的，因此使用偽隨機數加密的數據可能容易受到密碼分析的影響。 硬體隨機數生成器生成假定不可預測的數字序列，因此在用於加密數據時提供最大的安全性。
早期發展
產生隨機數的一種早期方法是用於播放基諾或選擇彩票號碼的相同機器的變體。這些混合編號的桌球帶著吹來的空氣，可能與機械攪拌相結合，並且使用一些方法從混合室中取出球（美國專利4,786,056）。這種方法在某些意義上給出了合理的結果，但是這種方法產生的隨機數是昂貴的。該方法固有地慢，並且對於大多數計算應用程式是不可用的。
1947年4月29日，蘭德公司開始生成隨機數字，帶有“電子輪盤”，由每秒約100,000個脈衝的隨機頻率脈衝源組成，每秒一次，恆定頻率脈衝，並送入五位二進制計數器。道格拉斯飛機公司製造了這種設備，實施了Cecil Hasting的建議（蘭德P-113）用於噪聲源（很可能是6D4微型氣體閘流管放置在磁場中時眾所周知的行為）。 32個可能的計數器值中的20個被映射到10個十進制數字上，而其他12個計數器值被丟棄。
蘭德機器長期運行，經過篩選和測試的結果被轉換成表格，該表格於1955年出版於“百萬隨機數字百萬正常偏差”一書中。 RAND表是提供隨機數字的重大突破，因為這樣一個大而精心準備的表從未有過。它一直是模擬，建模和導出加密算法中任意常數的有用資源，用於證明常量未被惡意選擇。塊密碼Khufu和Khafre是使用RAND表的應用程式之一。
具有隨機屬性的物理現象
量子隨機屬性
實際量子力學物理隨機性有兩個基本來源：原子或亞原子級的量子力學和thermal noise（其中一些是源自量子力學）。量子力學預測某些物理現象，例如原子的核衰變，基本上是隨機的，原則上不能預測（關於量子不可預測性的經驗驗證的討論，參見貝爾測試實驗）。並且，因為我們生活在絕對零度以上的溫度，所以每個系統的狀態都有一些隨機變化;例如，構成空氣的氣體分子不斷地以隨機方式相互反彈（參見統計力學）。這種隨機性也是一種量子現象。
由於量子力學事件的結果原則上無法預測，因此它們是隨機數生成的“黃金標準”。用於隨機數生成的一些量子現象包括：
•Shot noise，電子電路中的量子力學噪聲源。一個簡單的例子是照在光電二極體上的燈。由於不確定性原理，到達的光子在電路中產生噪聲。收集使用噪聲會帶來一些問題，但這是一個特別簡單的隨機噪聲源。然而，在整個感興趣的頻寬內，散粒噪聲能量並不總是很好地分布。橫向磁場中的氣體二極體和閘流管電子管可以產生大量的噪聲能量（10伏或更高的高阻抗負載）但具有非常高的能量分布，需要仔細過濾才能在廣譜範圍內實現平坦度。
•核衰變輻射源（例如，來自某些商業煙霧探測器），由連線到PC的蓋革計數器檢測。
•光子穿過半透明鏡子。檢測互斥事件（反射/傳輸）並分別與“0”或“1”位值相關聯。
•放大在反向偏置電晶體的基極上產生的信號。發射器被電子飽和，有時它們將穿過帶隙並通過基座離開。然後通過幾個電晶體放大該信號，並將結果饋入施密特觸發器。
•自發參量下變頻導致簡併光學參量振盪器中的二進制相位狀態選擇。
•通過零差檢測測量真空能量的波動。
經典隨機屬性
Thermal現象更容易檢測。雖然大多數系統將在足夠低的溫度下停止工作以將噪聲降低兩倍（例如，~150K），但它們在一定程度上容易受到降低系統溫度的攻擊。使用的一些熱現象包括：
•來自電阻器的thermal noise，被放大以提供隨機電壓源。
•Avalanche noise產生的avalanche diode，或來自Zener diode的Zener breakdown。
•由連線到PC的無線電接收器檢測到的Atmospheric noise（雖然大部分噪聲，例如閃電噪聲，但不是熱噪聲，但很可能是chaotic現象）。
在沒有量子效應或thermal noise的情況下，可以使用其他傾向於隨機的現象，儘管其方式不易以物理定律為特徵。當仔細地組合幾個這樣的源時（例如，在Yarrow算法或Fortuna CSPRNG中），可以收集足夠的熵用於創建加密密鑰和隨機數，儘管通常以受限的速率。優點是這種方法原則上不需要特殊的硬體。缺點是知識淵博的攻擊者可以偷偷地修改軟體或其輸入，從而可能大大降低輸出的隨機性。通常在這種方法中使用的主要隨機源是由機械輸入/輸出設備（例如鍵盤和磁碟驅動器，各種系統信息計數器等）引起的中斷的精確定時。
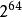硬體隨機數生成器
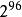硬體隨機數生成器必須謹慎實施最後一種方法，如果不是，可能會受到攻擊。例如，Linux 2.6.10核心中生成器的前向安全性可能會被或時間複雜度打破。
誤差處理
來自這些系統的比特流容易產生偏差，以1或0為主。有兩種處理偏差和其他偽像的方法。 第一種是設計RNG以最小化發電機運行中固有的偏差。 一種校正這種方法的方法是反饋由低通濾波器濾波的生成的比特流，以調整發生器的偏置。 通過中心極限定理，反饋迴路趨向於“幾乎所有次數”都經過良好調整。 超高速隨機數發生器通常使用這種方法。 即使這樣，產生的數字通常也有些偏頗。
軟體whitening
應對誤差的第二種方法是在生成後（在軟體或硬體中）減少偏差。即使採用了上述硬體偏差降低步驟，仍應假設比特流包含偏差和相關性。通過類似於從相關信號產生白噪聲的相關問題，存在幾種用於減少偏置和相關的技術，通常稱為“whitening”算法。另一種方法是動態靜態測試，它動態地對每個隨機數塊進行靜態隨機性檢查。這可以在短時間內完成，每秒1千兆位元組或更多。在這種方法中，如果一個塊被確定為可疑塊，則該塊被忽略並取消。 ANSI（X9F1）草案中要求使用此方法。
John von Neumann發明了一種簡單的算法來修復簡單偏差並降低相關性。它一次考慮兩個比特（非重疊），採取三種動作之一：當兩個連續的比特相等時，它們被丟棄;一個1,0的序列變成1;並且0,1的序列變為零。因此，它表示具有1的下降沿和具有0的上升沿。這消除了簡單的偏差，並且易於實現為電腦程式或數字邏輯。無論如何生成比特，該技術都有效。但是，它無法保證其輸出的隨機性。它能做什麼（具有大量丟棄比特）將偏置的隨機比特流變換為無偏比特流。
用於改善近似隨機比特流的另一種技術是對具有高質量密碼安全偽隨機數發生器（例如Blum Blum Shub或強流密碼）的輸出的異或比特流。這可以以低成本改善去相關和數字偏置;它可以通過FPGA等硬體完成，這比通過軟體實現的速度更快。
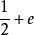硬體隨機數生成器
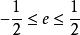硬體隨機數生成器
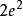硬體隨機數生成器減少近似隨機比特流中的偏差的相關方法是採用兩個或更多個不相關的近似隨機比特流，並將它們排除在一起。令比特流產生0的機率為，其中。然後e是比特流的偏差。如果具有偏差e的兩個不相關的比特流被排他地在一起，那么結果的偏差將是。這可以用更多比特流重複。
一些設計將加密散列函式（例如MD5，SHA-1或RIPEMD-160）或甚至CRC函式套用於全部或部分比特流，然後將輸出用作隨機比特流。這很有吸引力，部分原因是它與其他一些方法相比速度相對較快，但很大程度上取決於哈希輸出中的質量，而這些質量可能沒有什麼理論依據。
許多物理現象可用於生成高度偏差的位，但每個位獨立於其他位。蓋革計數器（採樣時間長於管恢復時間）或半透明鏡像光子探測器都會產生大多數為“0”（靜音或透射）的位流，偶爾會出現“1”（點擊或反射）。如果每個比特獨立於其他比特，則馮·諾依曼策略為這種高度偏置的比特流中的每個罕見的“1”比特生成一個隨機的無偏輸出比特。諸如高級多級策略（AMLS）等美白技術可以從這種高度偏差的比特流中提取更多的輸出比特 - 輸出比特就像隨機和無偏差的一樣。
PRNG定期刷新隨機密鑰
其他設計使用被認為是真隨機比特作為高質量分組密碼算法的關鍵，將加密輸出作為隨機比特流。但是，在這些情況下必須小心選擇合適的塊模式。在一些實現中，PRNG針對有限數量的數字運行，而硬體生成設備生成新種子。
