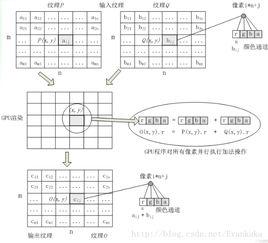
個別元素相加
通常的矩陣加法被定義在兩個相同大小的矩陣。兩個 m×n矩陣 A和 B的和，標記為 A+ B，一樣是個 m×n矩陣，其內的各元素為其相對應元素相加後的值。例如：
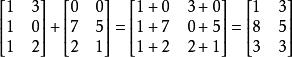矩陣加法也可以做矩陣的減法，只要其大小相同的話。 A- B內的各元素為其相對應元素相減後的值，且此矩陣會和 A、 B有相同大小。例如：
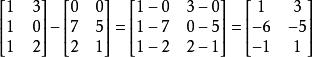矩陣加法做矩陣加法
一般的矩陣加（減）法如下，至於下一節的“直和”請另找參考資料。
先輸入要相加的兩個矩陣，大小必須一致為mxn，一般矩陣加法才有定義；
用滑鼠選取大小為的空白格矩陣；
輸入 =
用滑鼠選取矩陣1
輸入 + （若做減法則輸入 -）
用滑鼠選取矩陣2
1.先輸入要相加的兩個矩陣，大小必須一致為mxn，一般矩陣加法才有定義；
2.用滑鼠選取大小為的空白格矩陣；
3.輸入 =
4.用滑鼠選取矩陣1
5.輸入 + （若做減法則輸入 -）
6.用滑鼠選取矩陣2
7.按“Ctrl+Shift+Enter”這三個鍵的組合。
直和
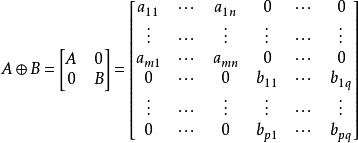矩陣加法另較少用來的一種運算為直和。直和可以由任何一對矩陣形成，其定義為：
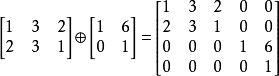矩陣加法舉例來說：
注意到兩個方陣的直和可以表示兩個圖論的聯集之鄰接矩陣。
在任兩個向量空間內取定基底，並取兩基底的聯集為向量空間直和的基底，則兩空間上的線性變換的直和可以表成兩矩陣的直和。
一般地， n個矩陣的直和可以寫成：
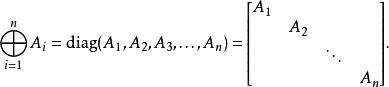矩陣加法