緒論
相空間表述理論是由希爾布蘭德·格倫尼伍爾德於1946年在其博士學位論文中提出的。 何塞·恩里科·穆瓦亞爾也在3年後獨立導出該理論。他們所提出的理論都建構於赫爾曼·外爾以及尤金·維格納早先的構想。
相空間表述的主要優勢在於其在形式上與哈密頓力學近似，可以避免引入算符，進而可以“令量子化問題擺脫希爾伯特空間的限制”。這一表述具有統計性質，表現了量子力學和經典統計力學邏輯上的聯繫，提供了一個比較二者的角度。相空間表述在量子光學、量子退相干以及一些特殊問題中已經得到套用，但其尚未得到廣泛套用。
相空間表述所基於的一些概念已在數學領域得到了進一步發展，如代數形變理論以及非交換幾何。
相空間分布
在相空間表述中，相空間分布，而非較為常見的波函式或是密度矩陣，是對於系統量子態最為基礎的描述方式。量子態 f( x, p)在相空間中的分布是一個準機率分布。
這一分布有許多種表象，而這些表象也是互相相關的。其中較為重要的一種是維格納準機率分布表象， W( x, p)。其他表象包括格勞伯-蘇德爾辛P表象、伏見Q表象、柯克伍德-雷阿切克表象、梅塔表象、里維耶表象以及玻恩-約當表象等等。其他表象在哈密頓算符取特定形式時會較為便利，如哈密頓算符取正規序時，採用格勞伯-蘇德爾辛P表象在演算時會較為簡便。由於維格納表象較為常用，因而在下文中，如不特殊提及，將統一採用該表象。
相空間分布性質與2 n維相空間機率密度分布類似。例如，其分布值是實數，這與通常是複數的波函式不同。我們可以通過在全動量域以及某一位置區間上的維格納函式積分來理解該位置附近的機率分布：
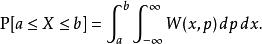相空間表述如果 Â( x, p)是一個表征可觀測量的算符，其可以通過維格納變換映射到相空間中，成為 A( x, p)，還可以通過外爾變換還原回來。
通過相空間分布可以求得可觀測量的期望值為：
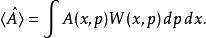相空間表述需要注意的是，儘管形式存在一定的類似性，但考慮到機率第三公理的要求 W( x, p)並非一種聯合分布，因為其所表征的區域中的狀態並不一定相互排斥。此外，儘管會違反機率第一公理，即使系統處於純態時，在特殊情況下，如系統處於相干態時，其值也可能為負。
可以證明，分布值為負的區域非常小，其對於系統整體的影響在幾ħ內，因而會在經典極限情況時會消失。但由不確定性原理，負分布值的區域有存在的可能性。不確定性原理並不允許對於相空間內小於ħ的區域進行精確描述。如果方程左邊為希爾伯特空間中算符的期望值，那么在量子光學領域，這個式子可以稱作光學等價性定理。
星積
相空間中基礎的二元非交換運算為穆瓦亞爾積，其對應標準的算符間乘法，以符號★表征，因而也稱“星積”。每種表象下，相空間分布所對應的星積運算法則也有所不同。下文中將討論維格納-外爾表象下的星積。
為了簡潔表記，在這裡引入左導數與右導數的標記方法。對於一對函式 f與 g，它們的左、右導數分別定義為：
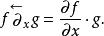相空間表述
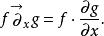相空間表述星積的微分定義為：
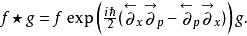相空間表述式中，指數函式可以理解為一個冪級數。
通過傅立葉變換還可以定義卷積積分形式的星積：
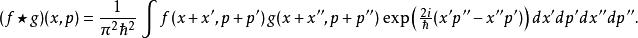相空間表述能量的本徵態分布一般稱作“星積本徵態”或是“星積本徵函式”，對應的能量值則被稱為“星積本徵值”。它們是對應含時薛丁格方程的星積本徵值方程的解：
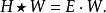相空間表述式中 H為哈密頓量。它是一個普通相空間函式，通常與經典力學中的哈密頓量相同。
時間演化
相空間的時間演化可以通過對劉維爾方程進行量子改造得到。這個方程是通過對馮諾伊曼方程進行維格納變換得到的。
對於相空間分布的任意表象及其對應的星積，存在：
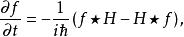相空間表述特別地，對於維格納函式，存在：
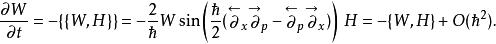相空間表述式中{{ , }}為穆瓦亞爾括弧。其為對易算符經過維格納變換後的結果，而{ , }則為經典力學中的泊松括弧。
而這個式子也服從對應原理：當 ħ→ 0時，這個方程將還原為經典力學中的劉維爾方程。然而，推廣至量子流情況時，相空間某一點的密度卻並不守恆，機率流也將發散且可壓縮。因而在這裡，量子軌道的概念會顯得有些微妙。
例子
簡單諧振子
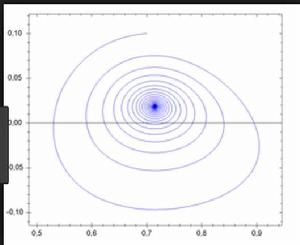
對於諧振子而言，任意的維格納分布的時間演化非常容易求得。初態為 W( x, p; t=0) = F( u)時的情況可以通過將上述結果在相空間中做剛性轉動求得：
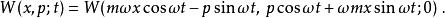相空間表述一般情況下，能量 E≫ ħω的量子諧振子可以表征巨觀諧振子。其在相空間中會做勻速運動。對其在全相空間中積分（起點為 t= 0），則可以得到一個連續的“圍欄”。其含時屬性與上面的靜態星積本徵態 F( u)相似，可以作為經典極限的直觀表現。
粒子角動量
假設粒子最初處於最小不確定高斯態，位置與動量的期望值在相空間原點。這種自由傳播的態的維格納函式為：
相空間表述式中， α為表征高斯波包的寬度的參數，而 τ= m/ α ħ。
最初，位置與動量並不相關。因而在三維情形下，位矢與動量是平行的，且大小為垂直情形的2倍。
然而，位置與動量的相關性會隨著狀態演化而越來越強，因為相對於原點傳播得越遠，動量值需要更大。這一情形的漸近式為：
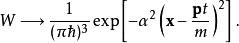相空間表述在這裡，只能求出粒子的動能的漸近解，與給定取向獨立性時的基態非零角動量情況一致：
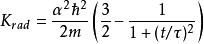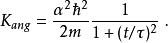相空間表述
相空間表述莫爾斯勢
莫爾斯勢常被用來近似雙原子分子的振動結構。
量子隧穿效應
量子隧穿效應是一種典型的量子效應。在發生隧穿時，粒子在不具備足夠飛躍勢壘的能量時，仍能像有一個“隧道”一樣穿過勢壘。這一效應在經典力學中並沒有對應的效應。
