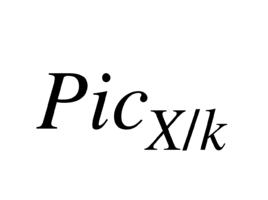簡介
皮卡概形是光滑代數簇X的皮卡簇(X)的概念在概形理論框架內的自然推廣。
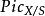 皮卡概形
皮卡概形為了對任意的S概形X定義皮卡概形。先要考慮概形S上的概形的範疇Sch/S里的相對皮卡函子(relative Picard functor)。這個函子在S概形S'上的值是一個群
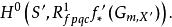 皮卡概形
皮卡概形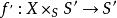 皮卡概形
皮卡概形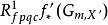 皮卡概形
皮卡概形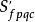 皮卡概形
皮卡概形這裡是基變換態射,是在嚴格平坦擬緊態射的格羅滕迪克拓撲里與預層
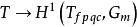 皮卡概形
皮卡概形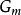 皮卡概形
皮卡概形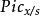 皮卡概形
皮卡概形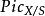 皮卡概形
皮卡概形相關聯的層,表示標準的乘法群層。如果皮卡函子是在Sch/S上可表示的,則表示它的 S 概形被稱為 S 概形的相對皮卡概形(relative Picard scheme),記為。如果 X 是某個域 k 上的代數概形,k有一個有理k點,則對任意 k 概形 S'有
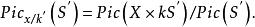 皮卡概形
皮卡概形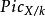 皮卡概形
皮卡概形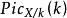 皮卡概形
皮卡概形特別地,X/k(k)=Pic(X)可被等同於的 k 有理點的群(如果這個群存在的話)。
性質
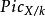 皮卡概形
皮卡概形如果f :X → S是具有幾何整纖維的射影態射,則概形存在而且是局部有限可表示的可分群S概形。
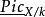 皮卡概形
皮卡概形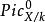 皮卡概形
皮卡概形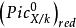 皮卡概形
皮卡概形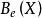 皮卡概形
皮卡概形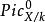 皮卡概形
皮卡概形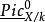 皮卡概形
皮卡概形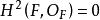 皮卡概形
皮卡概形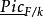 皮卡概形
皮卡概形如果S=Spec(k),則的單位連通分支是一個代數 k 概形,而且對應的約化 k 概形正式皮卡簇。概形的局部環里的冪零元給出了皮卡概形的許多附加的信息,而且能解釋在特徵數 p>0 的域上的代數幾何里的各種“病態”。另一方面,在特徵數0定域上概形總是約化的。當 F 是光滑代數曲面且時已經知道是一種約化概形。
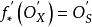 皮卡概形
皮卡概形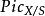 皮卡概形
皮卡概形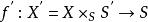 皮卡概形
皮卡概形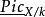 皮卡概形
皮卡概形對任何有的真平坦態射f :X → S(當基S為諾特時,它是有限可表示的),函子對於任何基變換態射是 S 上的代數空間。特別地,當基域 S 是局部阿廷環的譜時,函子是可表示的。