定義
白塞爾公式是利用最或然誤差求均方誤差的公式。
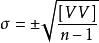 白塞爾公式
白塞爾公式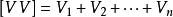 白塞爾公式
白塞爾公式從均方誤差的定義可知,均方誤差σ等於各觀測值的真誤差△平方和的算術平均值的平方根。但在實際工作中,真值是往往不知道的,真誤差當然也是不知道的。所以,求均方誤差的實用公式是白塞爾公式,即 ,式中σ為均方誤差,y為最或然誤差,n為觀測次數,[ ]為高斯取和符號。 。
算術平均值原理
設某量的真值為 x , n 次等精度觀測值為 l,l,…,l,其相應的真誤差為 ∆∆,…,∆,則可得:
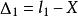 白塞爾公式
白塞爾公式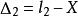 白塞爾公式
白塞爾公式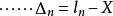 白塞爾公式
白塞爾公式將等式兩端分別相加並除以n,則
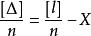 白塞爾公式
白塞爾公式令算術平均值:
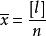 白塞爾公式
白塞爾公式並顧及偶然誤差的抵消性,即得:
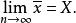 白塞爾公式
白塞爾公式因此,當觀測次數”趨於無限次時,算術平均值趨近於該量的真值。在實際工作中只能進行有限次觀測,算術平均值並不最接近於真值,但是比每一個觀測值更接近於真值,因此,通常認為有限次觀測值的算術平均值是該量的最可靠值,亦稱最或然值。
觀測值的改正數
算術平均值與觀測值之差,稱為觀測值的改正數,以v表示,即:
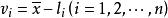 白塞爾公式
白塞爾公式將等式的兩端分別相加,得:
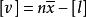 白塞爾公式
白塞爾公式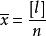 白塞爾公式
白塞爾公式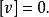 白塞爾公式
白塞爾公式顧及 可得
因此,在相同觀測條件下,一組觀測值的改正數之和恆等於零。這個結論常用於檢核計算。 ’
最小二乘法原理
最小二乘法原理是指在解算平差問題時,對一組互相獨立的等精度觀測值所施加之改正數的平方和應為最小,即
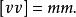 白塞爾公式
白塞爾公式換言之,應該在滿足上式的條件下求取最或然值。
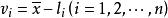 白塞爾公式
白塞爾公式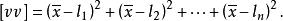 白塞爾公式
白塞爾公式由 得
根據最小二乘法原理,應使上式具有極小值,為此取一階導數,並令其等於零,得:
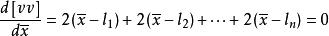 白塞爾公式
白塞爾公式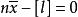 白塞爾公式
白塞爾公式故
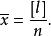 白塞爾公式
白塞爾公式因此,在等精度觀測的條件下,取觀測值的算術平均值作為最或然值,並由此得到各個觀測值的改正數是符合最小二乘法原理的。
