算法
以下虛擬碼展示了由遞歸地使用限制深度的 DFS (深度優先搜尋) 算法來實現的 IDDFS 算法 (叫作 DLS)。
特點
IDDFS結合了深度優先搜尋的空間效率和廣度優先搜尋的完整性(當分支因子是有限的時)。當路徑成本是節點深度的非遞減函式時,它是最佳的。
由於疊代加深訪問狀態多次,它可能看起來很浪費,但事實證明並不是那么昂貴,因為在樹中大多數節點都在底層,所以如果上層訪問多個並不重要倍。
IDDFS在遊戲樹搜尋中的主要優點是早期搜尋傾向於改進常用的啟發式方法,例如killer heuristic和alpha-beta pruning,以便在最終深度搜尋時更準確地估計各個節點的得分可以發生,並且搜尋完成得更快,因為它以更好的順序完成。例如,如果首先搜尋最佳動作,則alpha-beta pruning效率最高。
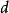 疊代深化深度優先搜尋
疊代深化深度優先搜尋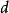 疊代深化深度優先搜尋
疊代深化深度優先搜尋第二個優點是算法的回響性。因為早期疊代使用 的小值,所以它們執行得非常快。這允許算法幾乎立即提供結果的早期指示,隨後在 增加時進行細化。當在互動式設定中使用時,例如在西洋棋遊戲程式中,該工具允許程式隨時使用在其已完成的搜尋中找到的當前最佳移動來播放。這可以表達為搜尋的每個深度都會逐漸產生更好的解決方案近似值,儘管每個步驟完成的工作都是遞歸的。對於傳統的深度優先搜尋,這是不可能的,這不會產生中間結果。
具體介紹
時間複雜度
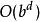 疊代深化深度優先搜尋
疊代深化深度優先搜尋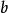 疊代深化深度優先搜尋
疊代深化深度優先搜尋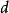 疊代深化深度優先搜尋
疊代深化深度優先搜尋在一個良好平衡的樹中IDDFS的時間複雜度與廣度優先搜尋相同,即 ,其中 是分支因子, 是目標的深度。
證明
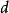 疊代深化深度優先搜尋
疊代深化深度優先搜尋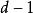 疊代深化深度優先搜尋
疊代深化深度優先搜尋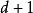 疊代深化深度優先搜尋
疊代深化深度優先搜尋在疊代加深搜尋中,深度 的節點展開一次,深度 的節點展開兩次,依此類推到搜尋樹的根部, 被展開 次。因此,疊代深化搜尋中的擴展總數是
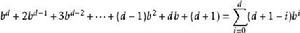 疊代深化深度優先搜尋
疊代深化深度優先搜尋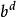 疊代深化深度優先搜尋
疊代深化深度優先搜尋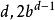 疊代深化深度優先搜尋
疊代深化深度優先搜尋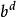 疊代深化深度優先搜尋
疊代深化深度優先搜尋其中 是深度展開次數 是深度{\ displaystyle d-1} d-1的擴展數,依此類推。 保理 給出
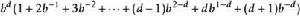 疊代深化深度優先搜尋
疊代深化深度優先搜尋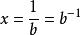 疊代深化深度優先搜尋
疊代深化深度優先搜尋讓 。 然後我們有
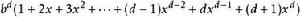 疊代深化深度優先搜尋
疊代深化深度優先搜尋這與無限序列相比少
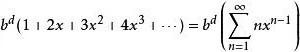 疊代深化深度優先搜尋
疊代深化深度優先搜尋合併後
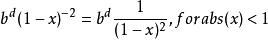 疊代深化深度優先搜尋
疊代深化深度優先搜尋然後我們可以得到
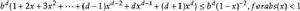 疊代深化深度優先搜尋
疊代深化深度優先搜尋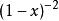 疊代深化深度優先搜尋
疊代深化深度優先搜尋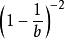 疊代深化深度優先搜尋
疊代深化深度優先搜尋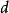 疊代深化深度優先搜尋
疊代深化深度優先搜尋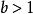 疊代深化深度優先搜尋
疊代深化深度優先搜尋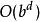 疊代深化深度優先搜尋
疊代深化深度優先搜尋自 或 是一個獨立於 (深度)的常數, 如果 (即,如果分支因子大於1),深度優先疊代加深搜尋的運行時間為 。
例子
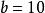 疊代深化深度優先搜尋
疊代深化深度優先搜尋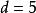 疊代深化深度優先搜尋
疊代深化深度優先搜尋對於 且 ,數字為
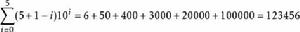 疊代深化深度優先搜尋
疊代深化深度優先搜尋 疊代深化深度優先搜尋
疊代深化深度優先搜尋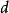 疊代深化深度優先搜尋
疊代深化深度優先搜尋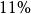 疊代深化深度優先搜尋
疊代深化深度優先搜尋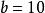 疊代深化深度優先搜尋
疊代深化深度優先搜尋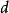 疊代深化深度優先搜尋
疊代深化深度優先搜尋總之,從深度 一直到深度 的疊代加深搜尋僅擴展 多個節點而不是單個廣度 - 當 時,第一次或深度限制搜尋到深度 。
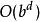 疊代深化深度優先搜尋
疊代深化深度優先搜尋分支因子越高,重複擴展狀態的開銷越低,但即使分支因子為2,疊代加深搜尋也只需要完整廣度優先搜尋的兩倍。 這意味著疊代加深的時間複雜度仍為 。
空間複雜度
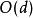 疊代深化深度優先搜尋
疊代深化深度優先搜尋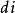 疊代深化深度優先搜尋
疊代深化深度優先搜尋IDDFS的空間複雜度是 ,其中是目標 的深度。
證明
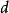 疊代深化深度優先搜尋
疊代深化深度優先搜尋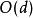 疊代深化深度優先搜尋
疊代深化深度優先搜尋由於IDDFS在任何時候都參與深度優先搜尋,因此它只需要存儲一堆節點,這些節點代表它正在擴展的樹的分支。 由於它找到了最佳長度的解,因此該堆疊的最大深度為 ,因此最大空間量為 。
通常,當存在大的搜尋空間且解決方案的深度未知時,疊代深化是首選的搜尋方法。
實例分析
如圖一所示:
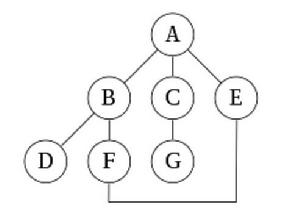 圖一
圖一從A開始的深度優先搜尋,假設在右邊緣之前選擇所示圖形中的左邊緣,並假設搜尋記住先前訪問過的節點並且保證不會重複(因為這是一個小圖),訪問節點的順序將按照以下形式:A,B,D,F,E,C,G。在此搜尋中遍歷的邊形成Trémaux樹,這是一種在圖論中具有重要套用的結構。
在不記住先前訪問過的節點的情況下執行相同的搜尋導致以A,B,D,F,E,A,B,D,F,E等順序訪問節點,永遠得到在A,B,D,F中 ,E循環,永遠不會達到C或G。
疊代加深會阻止此循環,並將在以下深度上到達以下節點,假設它從上到下依次進行:
•0: A
•1: A, B, C, E
(注意疊代加深已經得到了C,而傳統的深度優先搜尋沒有。)
•2: A, B, D, F, C, G, E, F
(注意,仍然得到C,但它後來出現。另請注意,它通過不同的路徑看到E,並循環回F兩次。)
•3: A, B, D, F, E, C, G, E, F, B
對於此圖,隨著更多深度的添加,兩個周期“ABFE”和“AEFB”將在算法放棄並嘗試另一個分支之前變得更長。
相關算法
與疊代深化相似的是一種稱為疊代延長搜尋的搜尋策略,它可以增加路徑成本限制而不是深度限制。 它按照增加路徑成本的順序擴展節點; 因此,它遇到的第一個目標是路徑成本最低的目標。 但疊代延長會產生大量開銷,使得它不如疊代加深那么有用。
疊代加深A *是最佳優先搜尋,其基於類似於在A *算法中計算的“f”值執行疊代加深。