總述
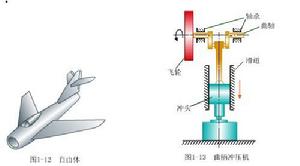理論力學研究示意圖理論力學是大部分工程技術科學的基礎，也稱經典力學。其理論基礎是牛頓運動定律。20 世紀初建立起來的量子力學和相對論，表明牛頓力學所表述的是相對論力學在物體速度遠小於光速時的極限情況，也是量子力學在量子數為無限大時的極限情況。對於速度遠小於光速的巨觀物體的運動，包括超音速噴氣飛機及宇宙飛行器的運動，都可以用經典力學進行分析。
理論力學從變分法出發，最早由拉格朗日《分析力學》作為開端，引出拉格朗日力學體系、哈密頓力學體系、哈密頓-雅克比理論等，是理論物理學的基礎學科。哈密頓方法是量子力學中的正則量子化的起點，拉格朗日方法是量子力學中路徑積分量子化的起點。
發展簡史
力學是最古老的科學之一，它是社會生產和科學實踐長期發展的產物。隨著古代建築技術的發展，簡單機械的套用，靜力學逐漸發展完善。公元前5—前 4世紀，在中國的《墨經》中已有關於水力學的敘述。古希臘的數學家阿基米德（公元前 3世紀）提出了槓桿平衡公式（限於平行力）及重心公式，奠定了靜力學基礎。荷蘭學者S.斯蒂文（16世紀）解決了非平行力情況下的槓桿問題，發現了力的平行四邊形法則。他還提出了著名的“黃金定則”，是虛位移原理的萌芽。這一原理的現代提法是瑞士學者約翰·伯努利於1717年提出的。
動力學的科學基礎以及整個力學的奠定時期在17世紀。義大利物理學家伽利略創立了慣性定律，首次提出了加速度的概念。他套用了運動的合成原理，與靜力學中力的平行四邊形法則相對應，並把力學建立在科學實驗的基礎上。英國物理學家牛頓推廣了力的概念，引入質量的概念，總結出機械運動的三定律（1687年），奠定了經典力學的基礎。他發現的萬有引力定律，是天體力學的基礎。以牛頓和德國人G.萊布尼茲所發明的微積分為工具，瑞士數學家L.歐拉系統地研究了質點動力學問題，並奠定了剛體力學的基礎。
理論力學發展的重要階段是建立了解非自由質點系力學問題的較有效方法。虛位移原理表示質點系平衡的普遍條件。法國數學家 J.達朗貝爾提出的、後來以他本人名字命名的原理，與虛位移原理結合起來，可以得出質點系動力學問題的分析解法，產生了分析力學。這一工作是由法國數學家J.拉格朗日於 1788年完成的，他推出的運動方程，稱為拉格朗日方程，在某些類型的問題中比牛頓方程更便於套用。後來愛爾蘭數學家W.哈密頓於19世紀也推出了類似形式的方程。拉格朗日方程和哈密頓方程在動力學的理論性研究中具有重要價值。
與動力學平行發展，運動學在19世紀也發展了。到19世紀後半葉，運動學已成為理論力學的一個獨立部分。
20世紀以來，隨著科學技術的發展，逐漸形成了一系列理論力學的新分支；並與其他學科結合，產生了一些邊緣學科，如地質力學、生物力學、爆炸力學、物理力學等。力學模型也越來越多樣化。在計算工作中，已廣泛採用了電子計算機，解決了過去難以解決的一些力學問題。
涵蓋內容
理論力學所研究的對象（即所採用的力學模型）為質點或質點系時，稱為質點力學或質點系力學；如為剛體時，稱為剛體力學。因所研究問題的不同，理論力學又可分為靜力學、運動學和動力學三部分。靜力學研究物體在力作用下處於平衡的規律。運動學研究物體運動的幾何性質。動力學研究物體在力作用下的運動規律。
理論力學的重要分支有振動理論、運動穩定性理論、陀螺儀理論、變質量體力學、剛體系統動力學、自動控制理論等。這些內容，有時總稱為一般力學。
理論力學與許多技術學科直接有關，如水力學、材料力學、結構力學、機器與機構理論、外彈道學、飛行力學等，是這些學科的基礎。
基本概念和方法
理論力學運動學中關於運動的量度，對於點有速度與加速度，對於剛體有移動的速度與加速度，轉動的角速度與角加速度。
物體間的相互機械作用的基本量度是力，理論力學中還廣泛用到力對點之矩和力對軸之矩的概念。
物體運動的改變除與作用力有關外，還與本身的慣性有關。對於質點，慣性的量度是其質量。對於剛體，除其總質量外，慣性還與質量在體內的分布狀況有關，即與質心位置及慣性矩、慣性積有關。剛體對於三個互相垂直的坐標軸的各慣性矩及慣性積組成剛體對該坐標系的慣性張量。
動力學中關於運動的量度有動量、動量矩和動能，與此有關的力的作用的量度有衝量、衝量矩和功。表明這兩種量度間的關係的定理，有動量定理、動量矩定理以及動能定理，稱為動力學普遍定理。
理論力學的基礎是牛頓三定律：第一定律即慣性定律；第二定律給出了質點動力學基本方程；第三定律即作用與反作用定律，在研究質點系力學問題時具有重要作用。第一、第二定律對於慣性參考系成立。在一般問題中，與地球固結的參考系或相對於地面作慣性運動的參考系，可近似地看作慣性參考系。
研究非自由質點系的平衡和運動的較有效方法是力學的變分原理，其中有虛位移原理、達朗貝爾原理、哈密頓原理等。在解題時廣泛套用了由此推出的運動微分方程，其中有拉格朗日方程、哈密頓正則方程、哈密頓-雅可比方程等。
靜力學
理論力學靜力學（statics）是研究作用於物體上力系的平衡條件的力學分支學科。力系指作用在物 體上的一群力。平衡指物體相對慣性參考系保持靜止或作等速直線運動。在靜力學中，將與地球固結的參考系取作慣性參考系可滿足一般工程所需的精度要求。靜力學研究的主要問題有三個。①物體的受力分析，即分析物體共受幾個力以及各力的作用點及方向。②力系的簡化，即用一個簡單的力系等效地替換一個複雜的力系。③力系的平衡條件，即力系與零力系等效的條件，此平衡條件用方程的形式表示時，稱為力系的平衡方程。如匯交力系的平衡條件是各力的合力為零，平衡方程則為各力在坐標軸上投影的代數和為零，即
∑F=0, ∑F=0, ∑F=0
矢量力學中主要研究作用於剛體上的力系平衡，故這一部分又稱為剛體靜力學，又因處理的是力、力矩等矢量的幾何關係，故又稱幾何靜力學。分析力學則研究任意質點系的平衡，給出作用於任意質點繫上的力系平衡的充要條件，即虛功原理，又稱分析靜力學。靜力學的研究方法是從幾條基本公理或原理出發，經過數學演繹推導出各種結論。
剛體是實際物體的簡化與抽象，工程中構件的變形影響可以忽略時，可套用剛體靜力學的理論。如設計橋樑桁架中各桿件的截面面積時，首先在規定載荷下用剛體靜力學的平衡方程求出支座的約束力及各桿的內力，然後才能進行強度、剛度分析與設計，對變形體（彈性體、塑性體、流體等）的平衡問題，除了考慮力和力矩的平衡條件，還要結合介質的變形特性。用分析靜力學研究變形體平衡時形成的能量法，在解決工程技術問題時也獲得了廣泛的套用。
靜力學的理論在動力學中也有重要套用。分析靜力學中的虛功原理與達朗貝爾原理相結合給出動力學普遍方程，它是推導非自由質點系各種運動微分方程的基礎。
動力學
動力學（dynamics）是研究物體機械運動與受力之間的關係的學科，力學的分支。自然界與工程中存在大量的動力學問題。研究動力學問題時，應首先進行分析、簡化，抽象成物理模型，再建立動力學方程，即物理模型的受力與運動之間的關係。這個過程稱為動力學建模，簡稱建模。對有限多自由度的離散系統，得到的是常微分方程；對無限多自由度的連續系統，得到的是偏微分方程。動力學問題通常有兩種提法：①已知系統的運動規律，求作用於系統的力。②已知系統的受力，求系統的運動規律。有時也有兩者的混合提法。運動微分方程有時有解析解，但多數情況下它們是非線性的，只能求數值解。
牛頓是動力學的奠基者，他於1687年提出了運動的三大定律（見牛頓運動定律），其中第二定律建立了動力學方程，由此可推導出動力學的三大定理：動量定理、動量矩定理與動能定理，它們都是用來建模及進行運動特性分析的有力工具。牛頓的工作及後來L.歐拉關於剛體動力學的研究，構成了經典力學的牛頓-歐拉體系，也是矢量力學的主要內容。
動力學基本規律的另一種敘述方法稱為達朗貝爾原理，它可看成牛頓第二定律的演變。依據達朗貝爾原理建立起來的動靜法是解決工程問題的一種實用方法。
牛頓運動定律發表100年後，J.拉格朗日建立了受完整約束的非自由質點系的動力學方程，稱為拉格朗日方程。拉格朗日及後來W.哈密頓等人的工作構成了分析力學的主要內容。如果說矢量力學以力作為核心概念，則分析力學將核心概念由力轉移到能量。在經典力學範圍內，以力為核心概念與以能量為核心概念是等價的；但在物理的其他領域，力與加速度的概念可能顯得沒有意義，而能量的概念卻無處不在。因此，分析力學成為由經典力學過渡到現代物理的橋樑。
根據研究對象的不同，動力學通常包括質點動力學、質點系動力學、剛體動力學及動力學專門問題幾個部分。
運動學
運動學（kinematics）是研究物體機械運動的幾何性質而不涉及運動的原因——物體的受力的力學分支。運動學的首要任務是描述物體相對所選參考系的運動，重點研究物體的軌跡、位移、速度、加速度等運動特性。運動學中只研究位置變化，不需要考慮質量。描述物體運動的一般方法是首先建立描述運動的運動方程，然後通過數學上對時間求導數獲得速度、加速度與運動特性。運動學與靜力學和動力學一起構成了力學的基礎，但運動學本身也有獨立存在的價值，如在機械設計中廣泛使用運動學知識分析或設計機構的運動。
