磨礦機的工作轉速
磨礦機的工作轉速n通常低於臨界轉速，通常將磨礦機工作轉速與臨界轉速之比的百分數稱為轉速率，用Ψ表示，即：
（5.4-4）
將公式代入，得到：
（5.4-5）
公式（5.4-5）指出，轉速率愈高，脫離角愈小，鋼球上升的位置也越高。當脫離角為0°時，轉速率為100%，即工作轉速等於臨界轉速，鋼球到達磨機的頂點，要開式離心運轉了。
磨礦機最適宜的轉速率目前尚無法確定，只有一些近似的理論計算，先簡單介紹如下：
（1）從外層鋼球具有最大落下高度出發，最適宜的轉速率為76%。在磨礦機內，鋼球落下衝擊礦石的能量來自它落到終點時的功能，而且功能大小，決定於剛球的落下高度。
A點為最外層球的脫離點，B點為最外層球的落回點，為脫離角。以脫離點A為原點，取坐標，則可列出最外層球上升的圓周運動軌跡方程式為：
轉速計算公式（5.4-6）
球從A點以初速度拋出，開式脫離筒體並以拋物先的軌跡向下降落，它的水平和垂直兩個方向上，在時間t內運行的距離為：
或
將值代入上式，得到 將式（5.4-1）代入上式，可得：
（5.4-7）
式（5.4-7）為鋼球落下時的拋物線軌跡方程式。解聯立方程（5.4-6）和（5.4-7）得落回點B的坐標為：
轉速計算公式（5.4-8）
上式中，符號表示B點在x坐標原點的下方。
球在拋物線軌跡上最高點C的坐標：因 ，故將式（5.4-7）取一次導數並令它等於零，可以找出C點的坐標和。
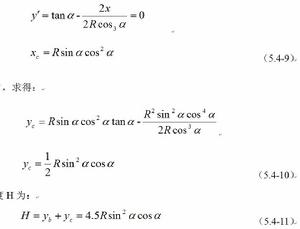轉速計算公式（5.4-9）
將代入式（5.4-7）中，求得：
即： （5.4-10）
最外層球的落下高度H為：
（5.4-11）
式（5.4-11）說明，球的落下高度H為脫離角的函式，有等於零可求得鋼球有最大拋落高度時，的脫離角。因此：
故： （5.4-12）
將值代入n=（30/R) 中得到最外層鋼球有最大落下高度時的磨礦機轉速為：
對應的轉速率為：
轉速計算公式（5.4-13）
這種理論值考慮最外層球處於適宜工作狀態，而其他層則未必處於適宜狀態，裝球越多，不適宜的球層也越多，故所求出的並不是最適應的轉速率。當磨機在該轉速率工作時，不能保證球荷在拋落狀態工作，只有低轉速工作的磨機才此採用此轉速率。
使中層（縮聚層）處於最有利工作狀態下工作的最適宜轉速率為88%。構想全部球荷的質量集中在某一球層，該球層稱為“縮聚層”（或中間層）。如果使該層球處於有利的工作狀態下（即該層的脫離角），則可認為全部球荷都處於理想的拋落狀態 。以 為該層球的脫離點，為落回點，為該層球層半徑，也就是全部球荷繞磨機中心作圓周運動的迴轉半徑。根據空心圓盤對O點的極轉動慣量半徑的求法，可以得到：
（5.4-14）
式中，K—最內層球半徑與最外層球半徑之比，；R1—最外層球的半徑R2—最內層球的半徑；R—磨機的內半徑，R=R1。
當中間層有最大拋落高度時，，則：
轉速計算公式（5.4-15）
使最內層球有明顯的圓周運動和拋物線運動所對應的最大脫離角為，所以最內層球的半徑為：
（5.4-16）
將式(5.4-15)和式（5.4-16）代入式（5.4-14）可得：
（5.4-17）
由式（5.4-15）和式（5.4-17）可得縮聚層處於適應工作狀態時磨礦機轉速為：
於是： （5.4-18）
及： （5.4-19）
這種理論考慮了全部球荷，多年來的生產實踐證明，在其他條件相同的情況下，磨礦機的轉速率為88%時較之76%時磨機的生產率要高些。
綜上所述，從理論上導出的球磨機的適宜轉速率為76%~88%,則適宜的工作轉速為：
轉速計算公式n=(0.76~0.88)n。 (5.4-20)
